CS/데이터베이스
[데이터베이스] 질의 최적화
rngPwns
2025. 6. 16. 08:15
11.1 질의 최적화 개요
📌 질의 최적화
사용자가 입력한 SQL문을 수행할 수 있는 여러 대안을 열거한 후,
대안들의 수행 비용을 예상하여 비교하고,
그중에서 가장 효율적인 대안을 선택하고 실행
📌 질의 최적화의 두 부분
- 대안들을 고려하면서 탐색 공간에 대한 가지치기(pruning)
- 고려 중인 각 계획의 비용을 예상
- SQL문에서 사용자는 원하는 것(what)을 명시하고,
사용자가 원하는 결과 데이터를 찾아오는 것(how)은 관계 DBMS의 역할

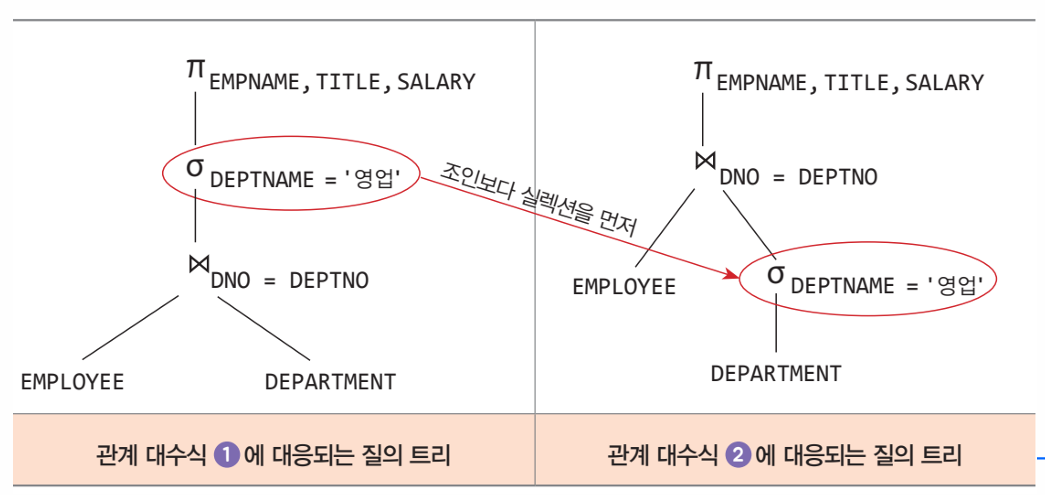
Q. 영업부에 근무하는 사원들의 이름, 직급, 급여를 검색하라.


- 관계 DBMS는 사용자가 입력한 SELECT문을 관계대수식으로 변환
- 동일 질의를 표현하는 여러 개의 관계대수식이 가능
- 관계대수식의 동등성을 이용하여 관계연산자들을 재배열해 좀 더 효율적인 관계대수식으로 만듦
- 대부분의 관계 DBMS는 관계대수식을 동등한 질의 트리(질의 계획)로 변환한 후 본격적인 최적화 작업을 진행

🔍 처리 순서
- EMPLOYEE와 DEPARTMENT를 먼저 조인
- 조인된 결과에서 DEPTNAME='영업'인 행만 선택
- 그 후 EMPNAME, TITLE, SALARY만 프로젝션(열 선택)
❗ 단점
- 조인을 먼저 수행하기 때문에 불필요한 많은 행이 생성될 수 있음
- 그 후에 '영업' 조건을 걸어서 필터링하므로 비효율적

🔍 처리 순서
- DEPARTMENT 테이블에서 먼저 DEPTNAME='영업'인 행만 선택
- 그 결과를 EMPLOYEE와 조인
- 필요한 열만 프로젝션
✅ 장점
- '영업' 부서만 미리 필터링하면 → 조인 대상이 줄어듦
- 즉, 조인 연산 비용이 확 줄어들어서 훨씬 효율적임
- 관계 DBMS는 사용자가 입력한 SELECT문을 관계대수식으로 변환
- 동일 질의를 표현하는 여러 개의 관계대수식이 가능
- 관계대수식의 동등성을 이용하여 관계연산자들을 재배열해 좀 더 효율적인 관계대수식으로 만듦
- 대부분의 관계 DBMS는 관계대수식을 동등한 질의 트리(질의 계획)로 변환한 후 본격적인 최적화 작업을 진행
✅ 관계 대수 기호 설명
| 기호 | 이름 | 뜻 |
| π (파이) | 프로젝션 (Projection) | **필요한 열(속성)**만 선택 |
| σ (시그마) | 셀렉션 (Selection) | **조건에 맞는 행(튜플)**만 선택 |
| ⨝ (조인) | 조인 (Join) | 두 테이블을 공통 속성 기준으로 연결 |
📌 질의 트리 (Query Tree)
- 관계대수식을 트리 형태로 표현한 것
- SELECT문이 관계대수식을 거쳐 동등한 질의 트리로 변환됨
- 각 질의 트리가 하나의 질의(수행) 계획에 해당함
- SELECT문의 FROM절에 포함된 테이블(들)이 질의 트리의 리프 노드
- 관계대수식의 단항 또는 이항 관계 연산자가 질의 트리의 내부 노드
- 내부 노드는 그것이 나타내는 관계연산자의 결과로 대체됨
- 관계연산자마다 여러 가지 수행 방법 중에서 선택된 수행 방법이 배정됨
- 질의 트리의 루트 노드는 맨 마지막에 수행되고, 주어진 질의 트리의 최종 결과로 대체됨

FROM R, S + WHERE R.B = S.B → R ⨝ S
| R.B = S.B | 조인 조건 → ⨝ 연산자 내부 (생략되기도 함) |
| S.C = v | 셀렉션 조건 → σ 연산자로 반드시 따로 표현 |

- 질의 트리에서 관계 연산자들의 순서를 바꾸는 여러 방법,
각 관계 연산자를 구현하는 여러 방법에 따라 다수의 질의 트리가 생성될 수 있음 - 관계 DBMS의 질의 최적화 모듈(query optimizer, 질의 최적화기)은
시스템 카탈로그에 유지되고 있는 다양한 통계정보를 활용하여
각 질의 트리의 예상 비용(자원 사용량)을 계산 - 관계 DBMS는 의미적으로 동등한 질의 트리들 중에서
예상 비용이 가장 적은 질의 트리를 선택하고,
이 질의 트리에 따라 실행파일(코드)을 생성한 후 수행함
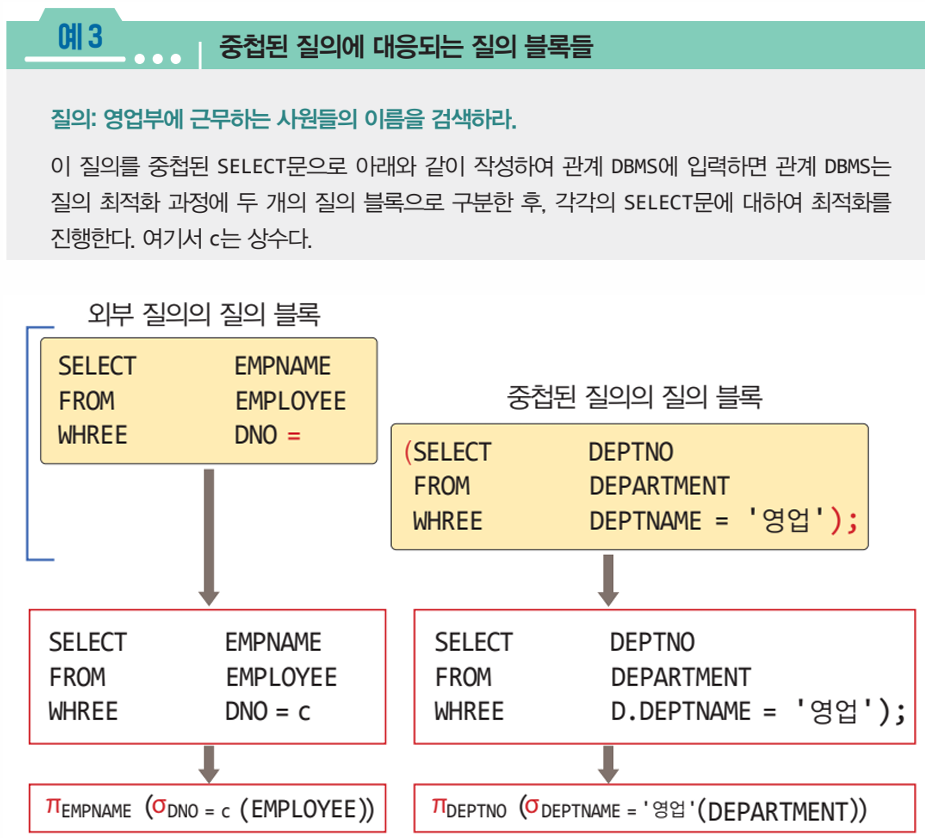
📌 질의 블록
- 중첩된 질의가 없는 하나의 SELECT문
- SELECT ... FROM ... WHERE ...의 구성요소들은 각각 관계 연산자인
프로젝션(π), 조인(⋈), 실렉션(σ)으로 변환됨


📌 질의 수행 단계
- 질의 파싱: 입력된 SELECT문을 내부 형식으로 파싱
→ 관계대수식으로 변환 후 질의 트리로 변환됨 - 질의 최적화:
효율적인 물리적 질의 계획을 찾는 과정
→ 논리적 질의 계획: 관계 연산자들로 표현된 질의 트리
→ 물리적 질의 계획: 각 노드에서 테이블 접근 경로(파일 스캔, 인덱스 등),
관계 연산자의 수행 방법을 추가
→ 논리적 질의 계획마다 여러 개의 물리적 질의 계획이 가능


관계대수식의 동등성



📌 비용 매개변수
- 질의 수행 비용 = 총 입출력 횟수
- 질의 최적화기가 효율적인 질의 계획을 선택할 때
주로 사용하는 시스템 카탈로그의 통계 정보

📌 경험 기반의 최적화 vs. 비용 기반의 최적화
▶ 경험 기반의 최적화
- 질의 계획을 항상 좋게 만드는 탐욕적(greedy) 규칙들을 적용
- 실렉션을 질의 트리에서 가능한 한 조인 연산자의 아래로 내려보냄
- 불필요한 컬럼 수(레코드의 길이)를 감소시키기 위해
프로젝션을 아래로 내려보냄 - 조인 결과가 작은 조인 연산을 먼저 수행하고,
카티션 곱은 회피함
- 프로젝션 (π, Projection 원하는 열(컬럼)
- 카티션 곱 (×, Cartesian Product) : 두 테이블의 모든 행을 조합해서 만드는 곱집합
- SQL의 FROM A, B (조인 조건 없이)와 같음
▶ 비용 기반의 최적화
- 각 질의 트리의 비용을 예상하기 위해 비용 기반 모델 사용
- 가능한 모든 질의 트리를 고려하지 않고 왼쪽 깊은 트리만 고려
- 이들 중 가장 작은 예상 비용을 갖는 트리를 선택
- 대부분의 관계 DBMS는 비용 기반 최적화기를 채택
- 현실적인 질의 최적화기의 목표는
반드시 최적은 아니더라도 효율적인 질의 수행 계획을 찾는 것,
또는 최악의 계획을 피하는 것

질의 수행 비용:
- EMPLOYEE 테이블의 TITLE 컬럼에 인덱스가 없으면,
실렉션(σTITLE='사원')을 수행하기 위해 EMPLOYEE 테이블의 모든 블록을 스캔해야 하므로
**B(EMPLOYEE)**만큼 디스크 입출력이 필요함. - 실렉션 조건을 만족하는 레코드가 넘어오면 바로바로 프로젝션을 수행할 수 있으므로
πEMPNAME, SALARY에 추가로 필요한 디스크 접근 횟수는 없음. - EMPLOYEE 테이블의 TITLE 컬럼에 인덱스가 있으면,
B+-트리 인덱스에서 첫 번째 사원 레코드를 찾는 데 2~4번의 입출력이 발생함.
이후, 다음 사원 레코드를 찾는 데 필요한 입출력 비용은
그 인덱스가 클러스터링 인덱스인지, 비클러스터링 인덱스인지에 따라 달라질 수 있음.- 인덱스가 있을 때, ‘사원’을 찾는 비용은 인덱스 종류에 따라 달라진다
어림짐작 (rule of thumb)

조건 만족하는 레코드 수를 미리 알 수 없을 땐,
선택률을 이런 공식으로 어림짐작해서
실행 계획의 비용을 계산하는 데 사용한다.
✅ 정리 표
조건 유형 선택률 인수 공식
| A = c | 1 / V(R, A) |
| A > c | (High - c) / (High - Low) |
| A = B | 1 / max(V(R, A), V(S, B)) |
✅ 11.3 왼쪽 깊은 트리
- 질의 최적화기가 모든 질의 트리를 고려할 수 없기 때문에,
수행 비용이 작은 질의 트리를 놓치지 않으면서 더 작은 탐색 공간으로 제한할 필요가 있음. - 왼쪽 깊은 트리는 오른쪽 가지가 항상 기본 테이블인 질의 트리를 말함.
- FROM절에 명시된 테이블의 개수가 n개일 때, 서로 상이한 왼쪽 깊은 트리는 n!개 가능함.


✅ 11.4 System R의 질의 최적화
- System R의 질의 최적화는 현재 가장 널리 사용되는 최적화 알고리즘임.
- 10개 미만의 테이블을 조인하는 SELECT문에서 잘 작동함.
- 비용 예상 모델은 매우 어림짐작 수준이지만 실제로는 잘 작동함.
- 연산의 비용 계산과 결과 크기를 예상하기 위해 시스템 카탈로그에 유지되고 있는 통계정보를 사용함.
- 비용 모델은 CPU 비용과 디스크 입출력 비용을 함께 고려함.

✅ 11.5 조인 알고리즘
📌 조인 알고리즘의 유형
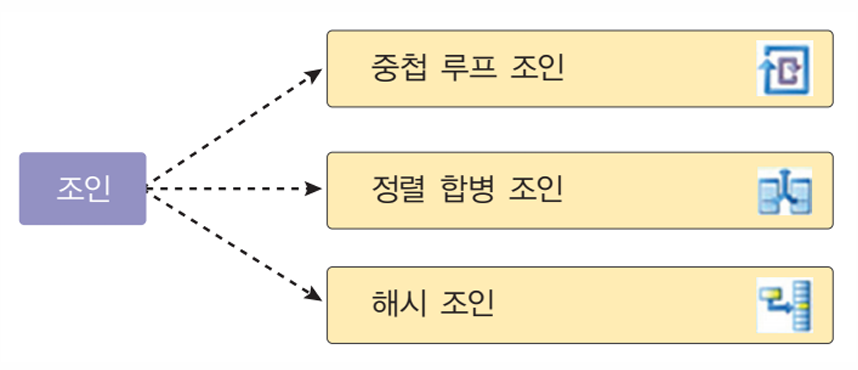
중첩 루프 조인 (NLJ: Nested Loop Join)
- FROM절에 명시된 두 테이블 R과 S 중 하나를 외부 테이블,
다른 하나를 내부 테이블로 정하고,
두 테이블의 레코드들이 조인 조건을 만족하는지 검사함.

레코드 기반 NLJ
- R ⋈ S
→ 조인 연산자 ⋈의 왼쪽 R이 외부, 오른쪽 S가 내부 테이블. - 단, 명시된 테이블 순서를 최적화기가 무조건 따르는 것은 아님.
즉, 다음 두 논리적 질의 트리 모두 생성 가능:

- 테이블 R, S의 조인 컬럼에 인덱스가 없어도 되고, 어떤 조인 조건(세타 조인)에도 적용 가능함.

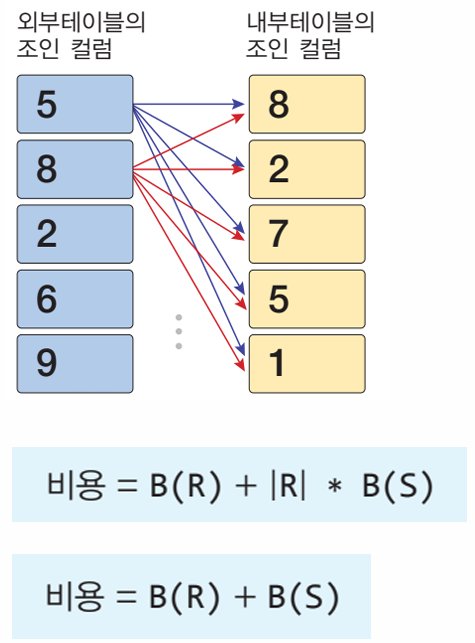

페이지(블록) 기반 NLJ
- 외부/내부 테이블 모두 디스크에서 버퍼로 읽는 단위는 블록임.
- R의 각 페이지마다 S의 페이지들을 읽어오고,
R-페이지의 레코드 r과 S-페이지의 레코드 s가
조인 조건을 만족하면 <r, s>를 결과 테이블에 포함함.
인덱스 NLJ
- 내부 테이블 S의 조인 컬럼에 인덱스가 있고 동등 조인일 경우,
내부 테이블에 대해 더 효율적인 인덱스 조회로 대체 가능함. - R과 S 둘 다 조인 컬럼에 인덱스가 있다면,
레코드 수가 적은 쪽을 외부 테이블로 설정함. - 외부 테이블 R을 스캔하며,
R의 각 레코드마다
S에서 조인 조건을 만족하는 레코드를 인덱스를 이용해 조회함. - c는 B+-트리 인덱스를 통해 S에서 레코드 1개를 조회하는 비용임.
정렬-합병 조인 (Sort-Merge Join)
- R과 S를 스캔하며
조인 컬럼 기준으로 정렬하고,
정렬된 R과 S를 병합하여 조인함. - 조인 조건을 만족하는 <r, s>는 결과에 포함됨.
- 조인 조건이 동등 조인일 때만 사용 가능.
- 두 테이블 중 하나 또는 둘 다 조인 컬럼으로 이미 정렬되어 있을 때,
또는 ORDER BY 절이 있는 경우 유용함.
외부 정렬
- 버퍼에 안 들어가는 대용량 테이블을 정렬할 때 사용함.
- 패스 0:
정렬되지 않은 테이블을 M블록씩 버퍼로 읽고
내부 정렬 후 디스크에 기록. - 패스 1:
M페이지 중 1페이지는 출력 런 저장용,
나머지 (M-1)페이지는 입력 런용.
M블록 런 × (M-1)개 → (M-1)×M 크기의 런 생성. - 패스 2: 이어서 더 큰 런들을 병합.
정렬-합병 알고리즘의 비용 분석
- ❖ 정렬-합병 알고리즘의 비용:
해시 조인 (Hash Join)
- R을 스캔하여 해시 버킷 생성
- S도 같은 방식으로 해시 버킷 생성
- 같은 버킷에 속한 R, S 레코드끼리
조인 조건 비교 → 만족하면 결과에 포함
해시 조인 (계속)
- 버퍼 용량이 M페이지일 때
1페이지는 R 또는 S의 블록을 읽어오는 용도,
나머지 (M-1)페이지는 해시 버킷 저장용. - R 블록을 읽어오고
각 레코드에 대해 해시 함수 h(key) mod (M-1) 적용.
→ 나머지가 0이면 버킷 0, 1이면 버킷 1, ..., (M-2)이면 버킷 (M-2)에 저장. - 버킷이 꽉 차면 디스크로 내보냄.
→ 같은 방식으로 S도 처리.
해시 조인 (계속)
- 같은 번호 버킷의 레코드들끼리만 조인 비교하므로
대각선 방향의 비교만으로 성능이 좋아짐. - ❖ 해시 조인 알고리즘의 비용: