[Database] ch06. 관계 데이터 연산

<연습문제 - ERgram 그리기>

* 156p 연습문제 28번

 

대학에서 학생은 교수에게 진로 지도를 받는다. 또한 학생들 간에도 멘토링을 실시하고 있는데 누구나 멘토 또는 멘티가 될 수 있다. ER diagram으로 표현해보세요. 단 외래키 속성이 무엇인지 표시 바랍니다.

 

<데이터베이스 스키마>

학생(학번_pk, 이름, 학과)

교수(교수 ID_pk, 이름, 학과)
지도(지도교수ID_pk, 참여학생_pk, 내용)

멘토링(멘토_pk, 멘티_pk, 내용)

 

<조건>

• 진로 지도를 담당하지 않는 교수가 있을 수 있다.
• 진로 지도를 받지 않는 학생이 있을 수 있다.
• 멘토링 프로그램에 멘토 또는 멘티로 참여하지 않는 학생이 있을 수 있다.

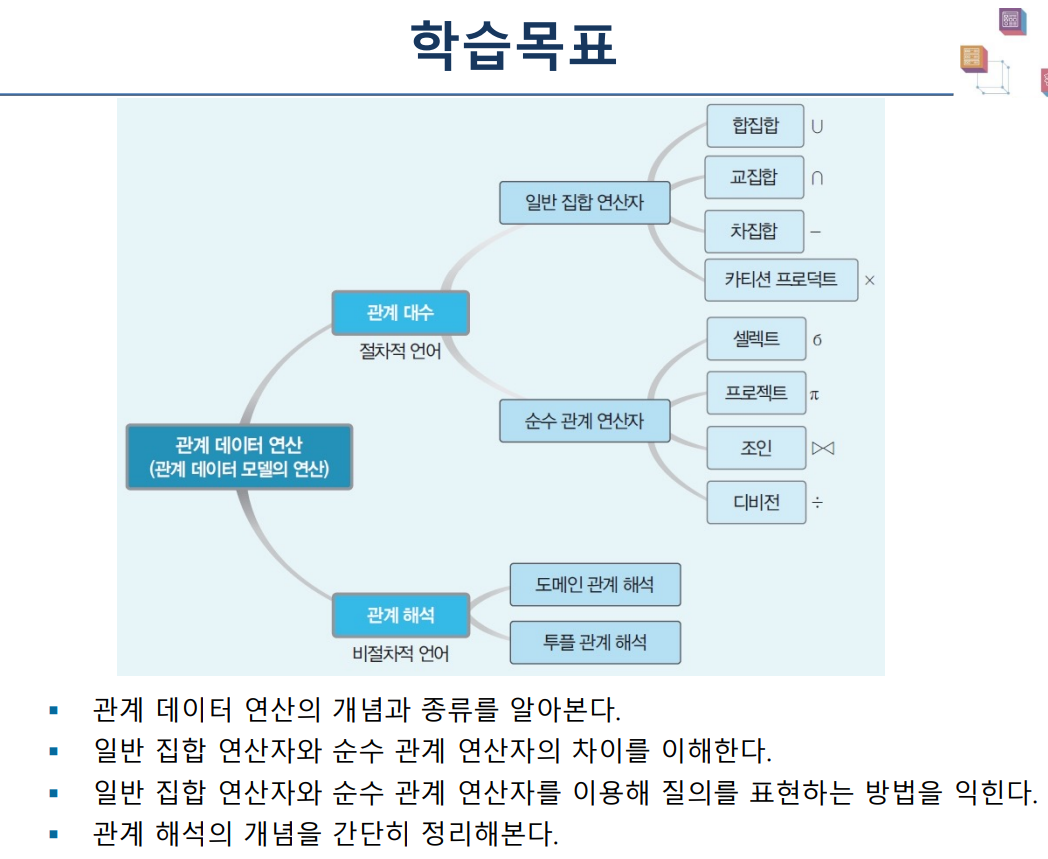
1. 관계 데이터 연산의 개념

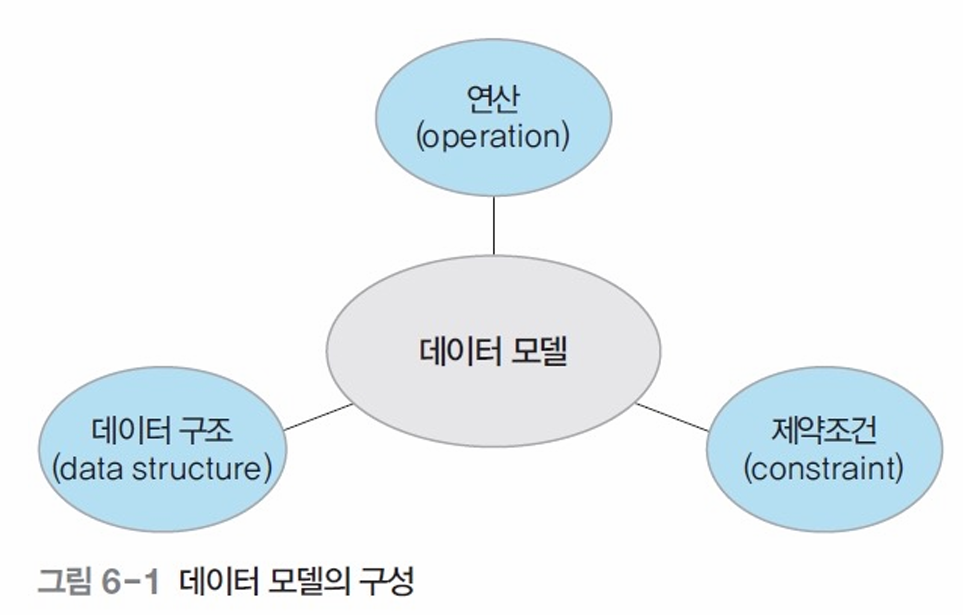
• 데이터모델 = 데이터 구조 + 연산 + 제약조건

 

관계 데이터 연산(relational data operation)

• 관계 데이터 모델의 연산
• 원하는 데이터를 얻기 위해 릴레이션에 필요한 처리 요구 수행
• 관계대수와 관계해석 : 기능과 표현력 측면에서 동등한 능력

 

• 관계 대수와 관계 해석의 역할
  • 데이터 언어의 유용성을 검증하는 기준
  • 관계 대수나 관계 해석으로 기술할 수 있는 모든 질의를 기술할 수 있는 데이터 언어 -> 관계적으로 완전(relationally complete) 하다고 판단
    • 질의 (query) : 데이터에 대한 처리 요구

관계 대수(relational algebra) 의 개념

• 절차 언어(procedural language) : 원하는 결과를 얻기 위해 릴레이션의 처리 과정을 순서대로 기술하는 언어
• 릴레이션을 처리하는 연산자들의 모임
  • 대표 연산자 8개 - 일반집합 연산자와 순수관계 연산자로 분류
• 폐쇄 특성(closure property)
  
  • 어떤 relation과 relation 대상으로 연산했던 결과 = relation. 이를 또 다른 연산의 피연산자로 사용.
  • 피연산자도 릴레이션이고 연산의 결과도 릴레이션 (부속 질의문 - sub-query)

 

관계대수의 연산자

 

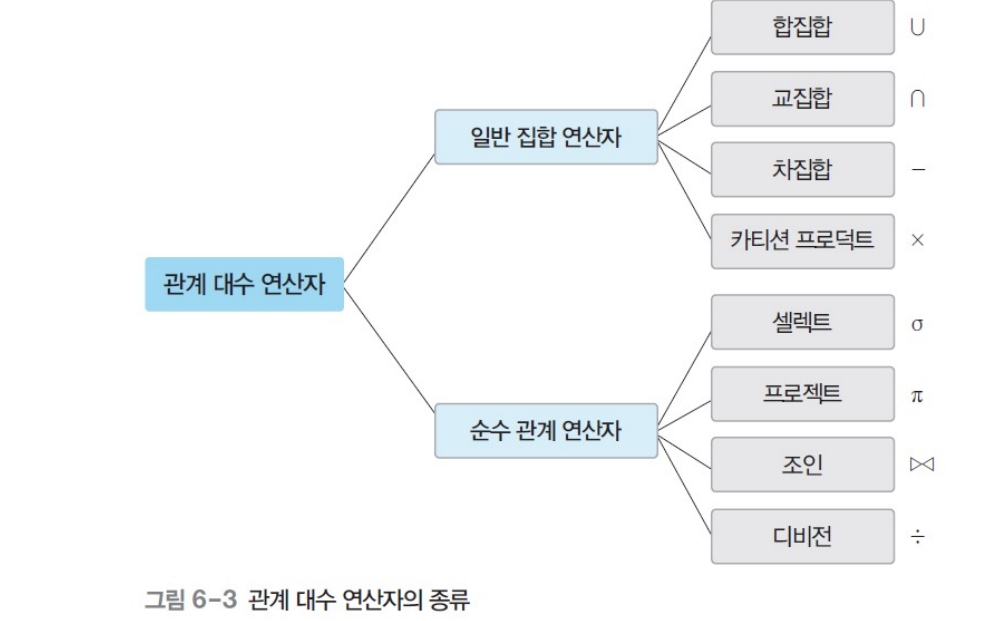
일반 집합 연산자(set operation)

• 릴레이션이 투플의 집합이라는 개념을 이용하는 연산자

 

특성

• 피연산자가 2개 필요 : 2개의 릴레이션을 대상으로 연산 수행
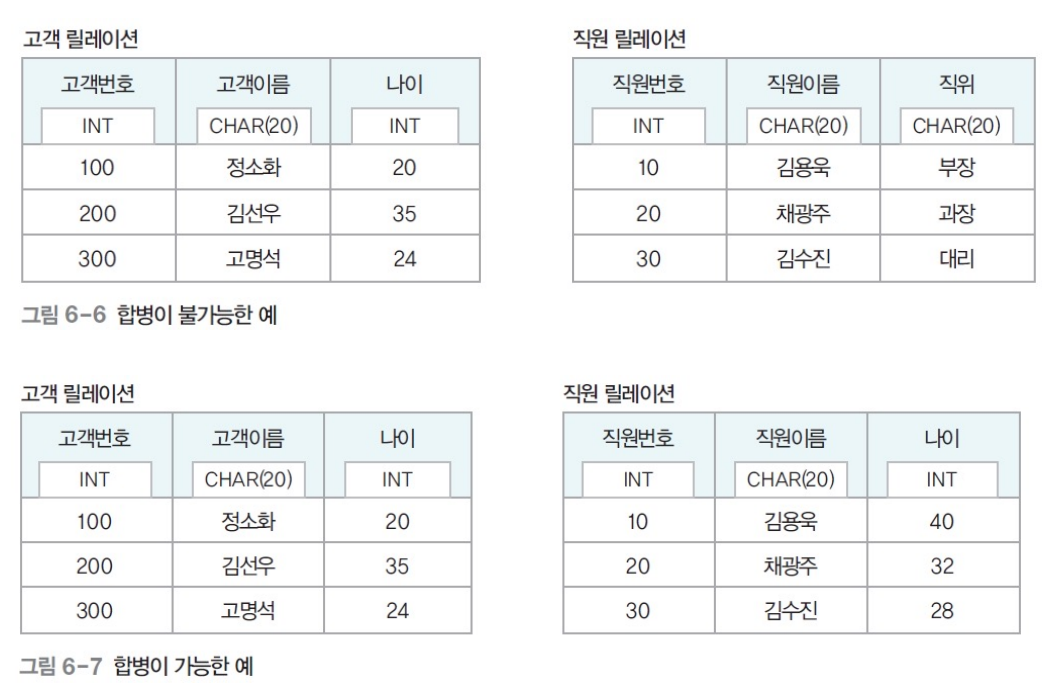
• 합집합, 교집합, 차집합은 피연산자인 두 릴레이션이 합병 가능해야 한다.
  • 합병 가능(union-compatible) 조건
    • 두 릴레이션의 차수가 같아야 한다.
    • 두 릴레이션에서 서로 대응되는 속성의 도메인이 같아야 한다.

합병 가능한 예 - 릴레이션의 차수 : 3

 

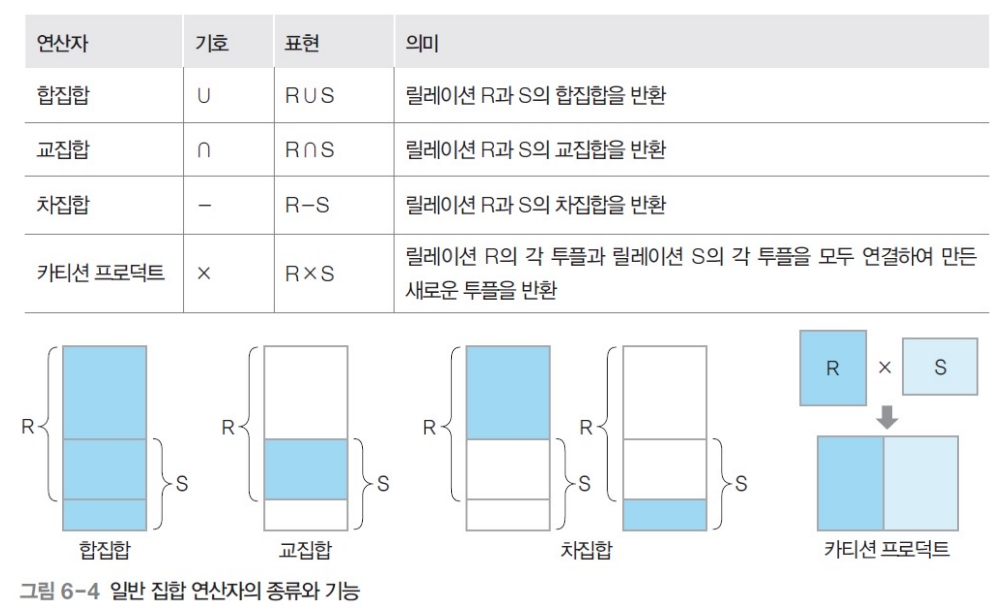
일반 집합 연산자 - 합집합(union)

• 합병 가능한 두 릴레이션 R과 S의 합집합 : R U S
  • 릴레이션 R에 속하거나 릴레이션 S에 속하는 모든 투플로 결과 릴레이션 구성
• 결과 릴레이션의 특성
  • 차수는 릴레이션 R과 S의 차수와 같음
  • 카디널리티는 릴레이션 R과 S의 카디널리티를 더한 것과 같거나 적어짐
• 교환적 특징 : R U S = S U R
• 결합적 특징 : (R U S) U T = R U (S U T)
• |R U S| <= |R| + |S|

 

 

 

일반 집합 연산자 - 차집합(difference)

• 합병 가능한 두 릴레이션 R과 S의 차집합 : R-S
  • 릴레이션 R에는 존재하지만 릴레이션 S에는 존재하지 않는 투플로 결과 릴레이션 구성
• 결과 릴레이션의 특성
  • 차수는 릴레이션 R과 S의 차수와 같음
  • R-S의 카디널리티는 릴레이션 R의 카디널리티와 같거나 적음
  • S-R의 카디널리티는 릴레이션 S의 카디널리티와 같거나 적음
• 교환적, 결합적 특징 X. (교환법칙 성립 X -> 결합법칙 성립 X)

 

일반 집합 연산자 - 카티션 프로덕트(cartesian product)

• 두 릴레이션 R과 S의 카디션 프로덕트: R x S
  • 릴레이션 R에  속한 각 투플과 릴레이션 S에 속한 각 투플을 모두 연결하여 만들어진 새로운 투플로 결과 릴레이션 구성
• 결과 릴레이션 특성
  • 차수 : 릴레이션 R,S의 차수를 더한 것과 같음
  • 카디널리티 : 릴레이션 R과 S의 카디널리티를 곱한 것과 같음
• 교환적 특징 O
  • RxS = SxR
• 결합적 특징 O
  • (RxS)xT = Rx(SxT)

 

순수 관계 연산자(relational operation)

• 릴레이션의 구조와 특성을 이용하는 연산자

 

 

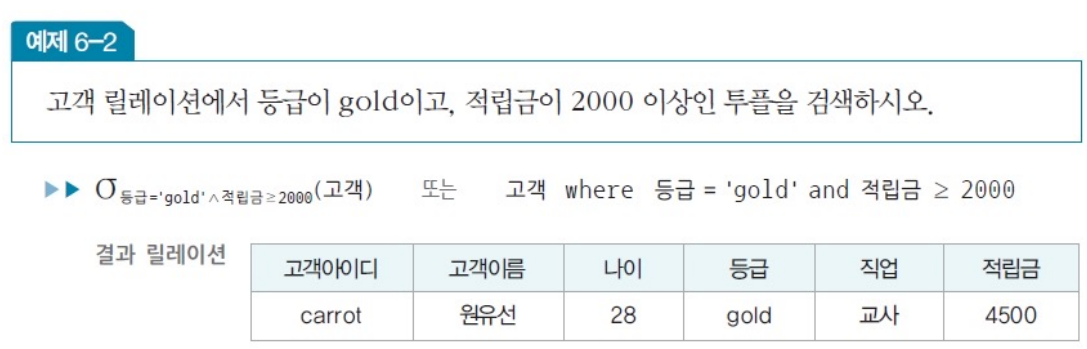
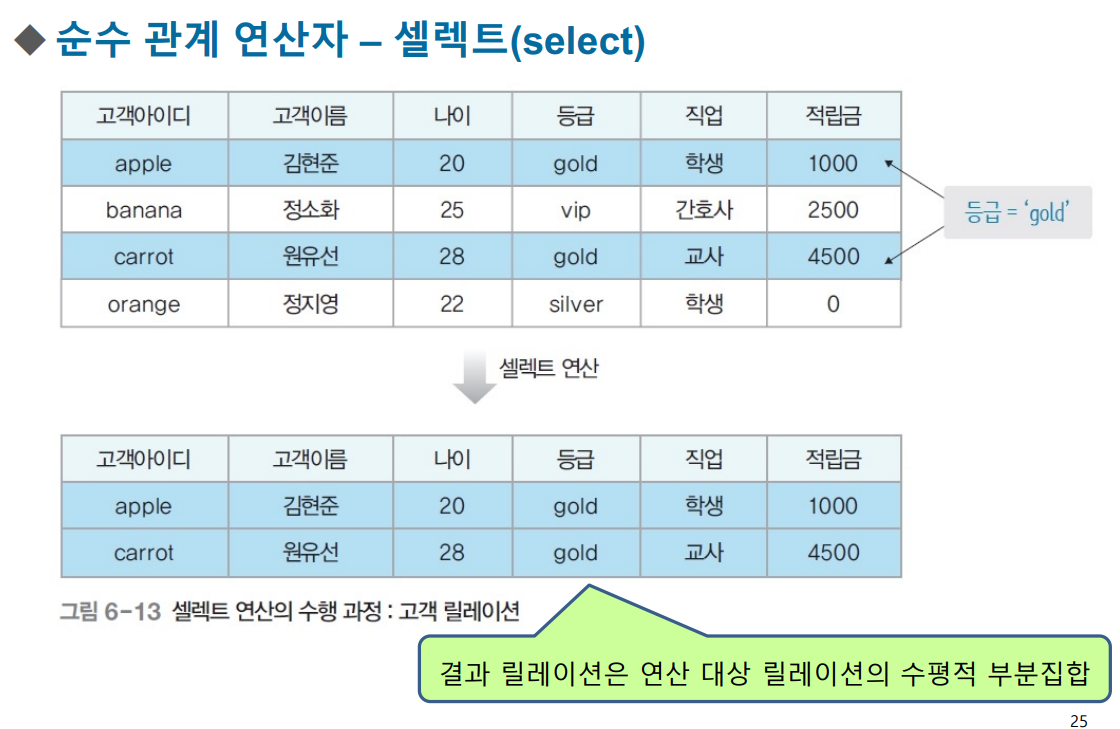
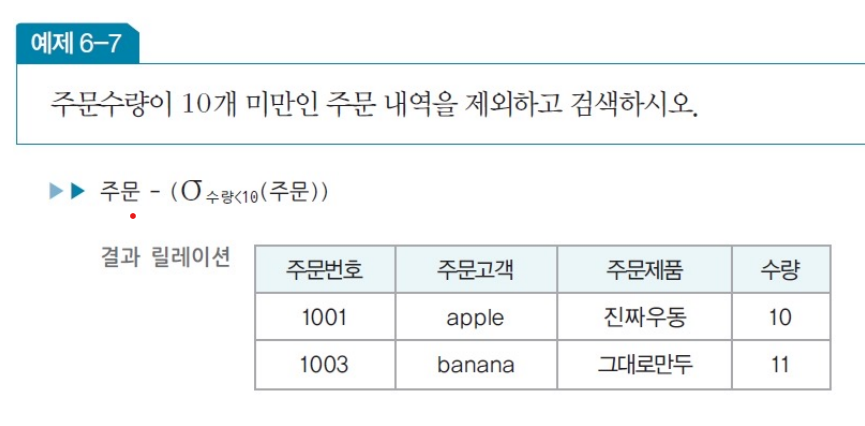
순수 관계 연산자 - 셀렉트(select)

• 릴레이션에서 조건을 만족하는 투플만 선택 -> 결과 릴레이션 구성
  • 수평적 연산자 : 결과 릴레이션은 연산 대상 릴레이션의 수평적 부분집합
• 하나의 릴레이션을 대상으로 연산 수행 연산을 수행
• 수학적 표현 : σ조건식(릴레이션) --> 시험에서 관계대수에 대해 물어볼 땐 얘 사용!
• 데이터 언어적 표현 : 릴레이션  where 조건식 --> SQL 에서만 사용
• 조건식
  • 비교식, 프레디킷(predicate) 이라고도 한다.
  • 속성과 상수의 비교나 속성들 간 비교로 표현
  • 비교 연산자 (>, ≥, <, ≤, =, ≠) 와 논리 연산자 (∧, ∨, ¬)를 이용해 작성

 

 

 

where 조건절 이하의 조건식이 표현

 

 

순수 관계 연산자 - 프로젝트(project)

• 릴레이션에서 선택한 속성의 값으로 결과 릴레이션 구성
  • 수직적 연산자 : 결과 릴레이션은 연산 대상 릴리이션의 수직적 부분집합
• 하나의 릴레이션을 대상으로 연산 수행
• 수학적 표현 : ㅠ속성리스트(릴레이션)
• 데이터 언어적 표현 : 릴레이션[속성리스트]

릴레이션에서는 투플의 중복 허용 x. -> 등급의 중복되는 투플을 자동으로 제거해준다.

사용 DBMS에서 검증하는 방향으로 사용. 똑같이 표현 :

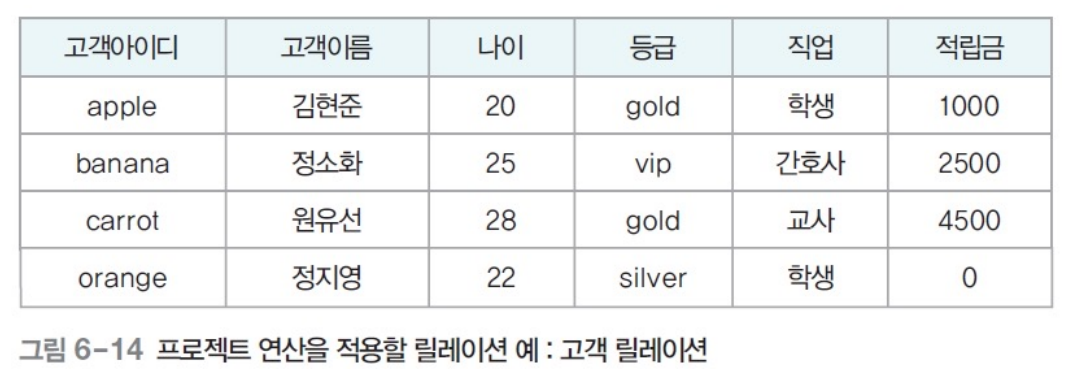
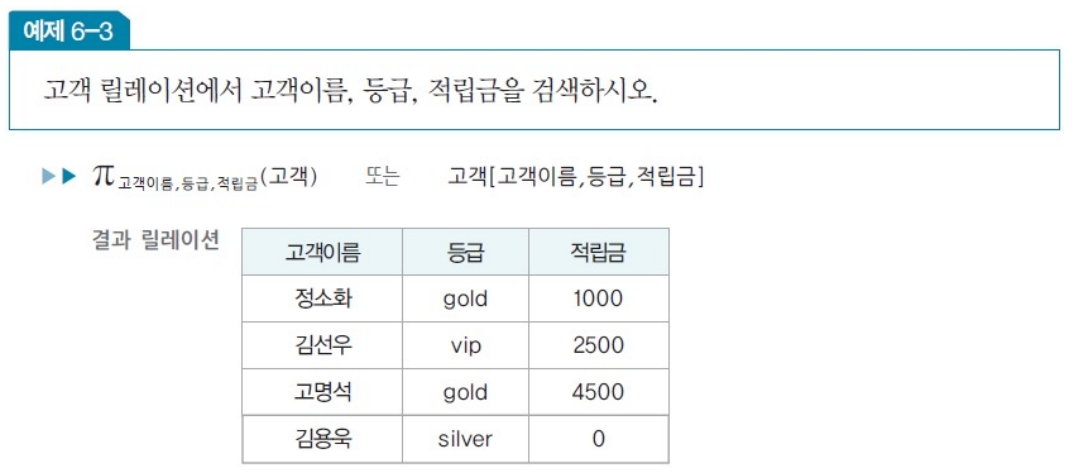
• 이론적으로는 중복 허용 x, 상용 DBMS에서는 gold vip gold silver 이렇게 나옴(테이블)
  • '중복 제거해주세요' 명령 덧붙이긴 할 수 있다. 

 

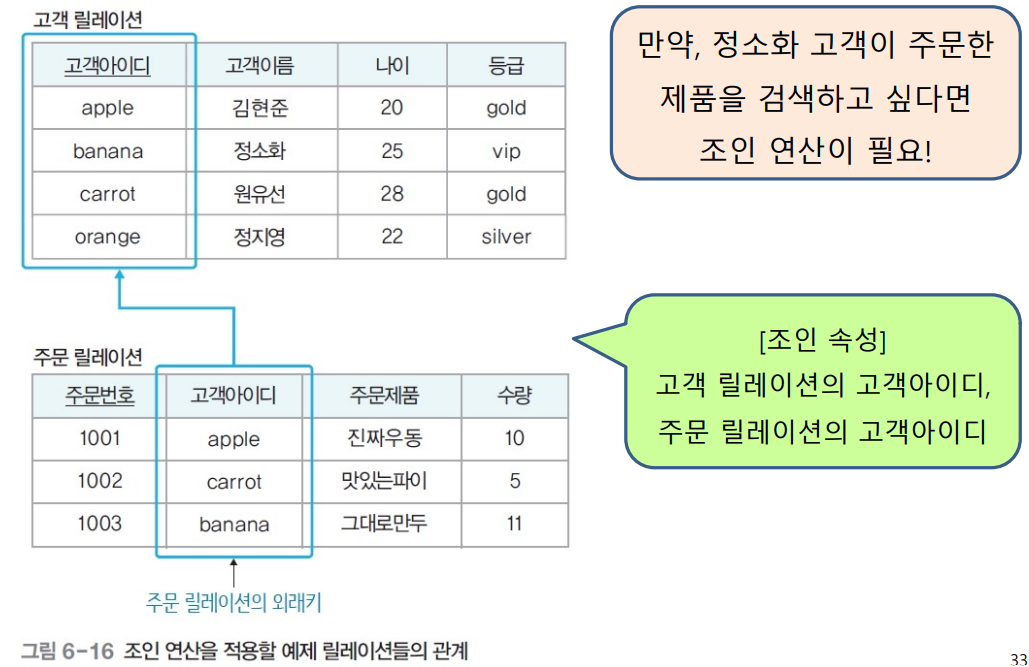
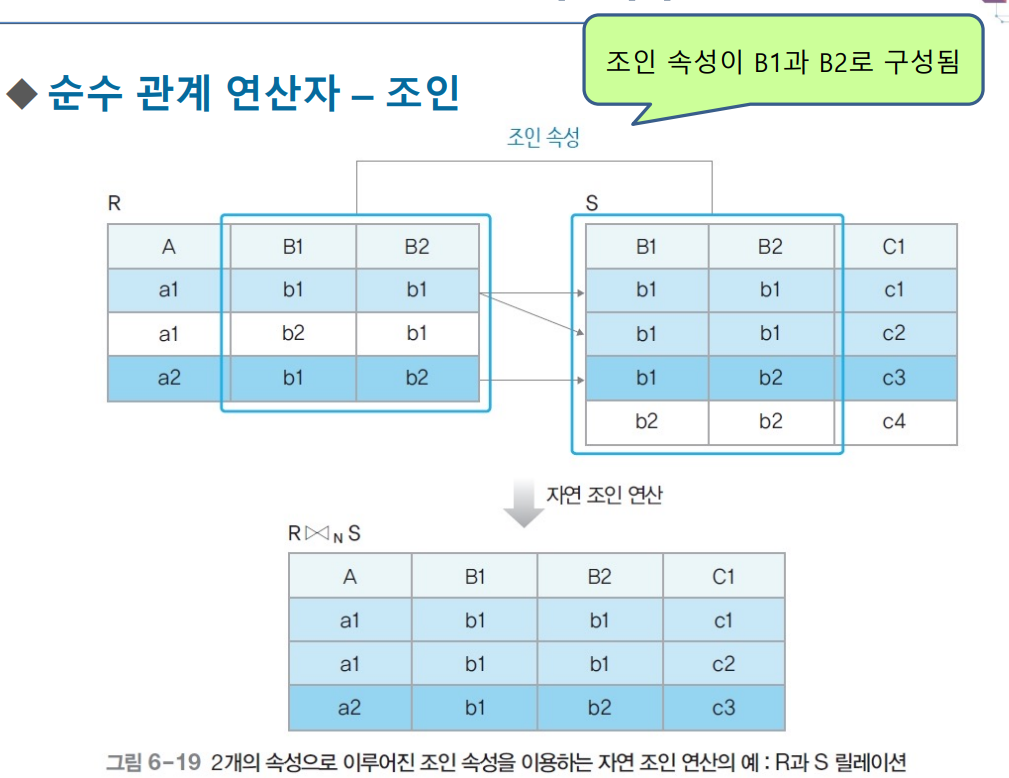
순수 관계 연산자 - 조인(join)

• 조인 속성을 이용해 두 릴레이션 조합 -> 결과 릴레이션 구성
  • 조인 속성의 값이 같은 투플만 연결해서 생성된 투플을 결과 릴레이션에 포함
  • 조인속성 : 두 릴레이션이 공통으로 갖고 있는 속성
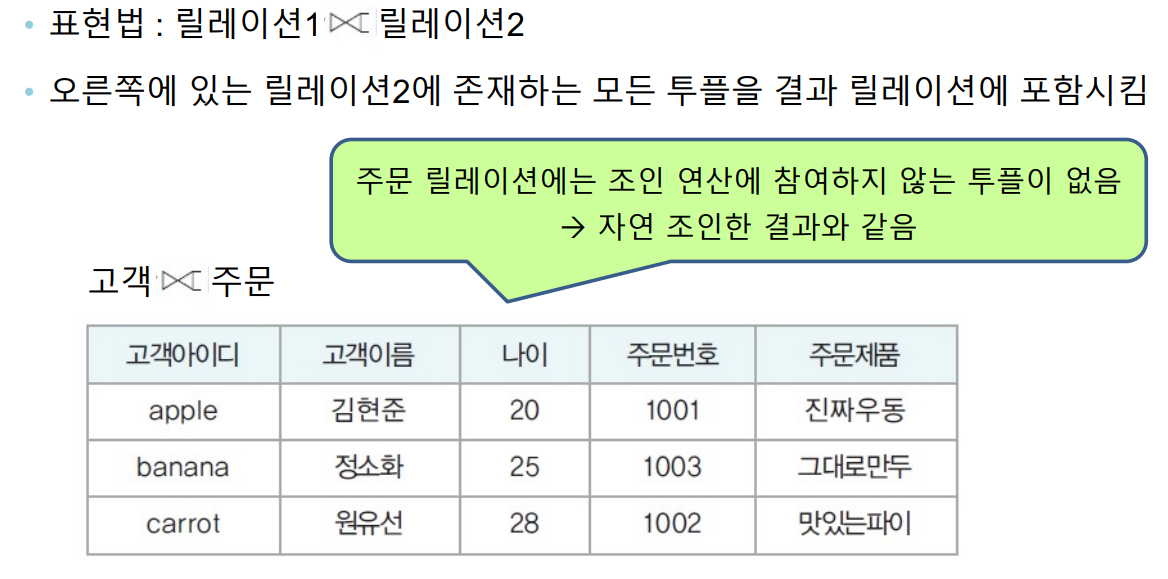
• 표현법 : 릴레이션1 ⋈ 릴레이션2
• 대부분 같은 형태로 조인 -> 동등 조인(equal-join) 이라고도 한다.

 

 

• 세타조인(theta θ  -join)
  • 동등 조인에 비해 더 일반화된 조인
  • 주어진 조인 조건을 만족하는 두 릴레이션의 모든 투플 연결하여 생성된 새로운 투플로 결과 릴레이션 구성
  • 결과 릴레이션의 차수는 두 릴레이션의 차수를 더한 것과 같다.
  • 표현법 : 릴레이션1 ⋈A θ B 릴레이션2
    • θ 는 비교 연산자(>, ≥, <, ≤, =, ≠)를 의미
• 동등조인(equi-join)
  • θ 연산자가 "='인 세타조인 의미
  • 표현법 : 릴레이션1 ⋈A=B 릴레이션2

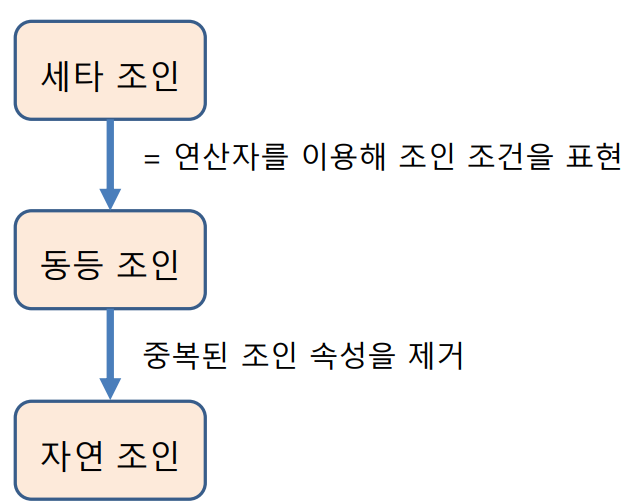
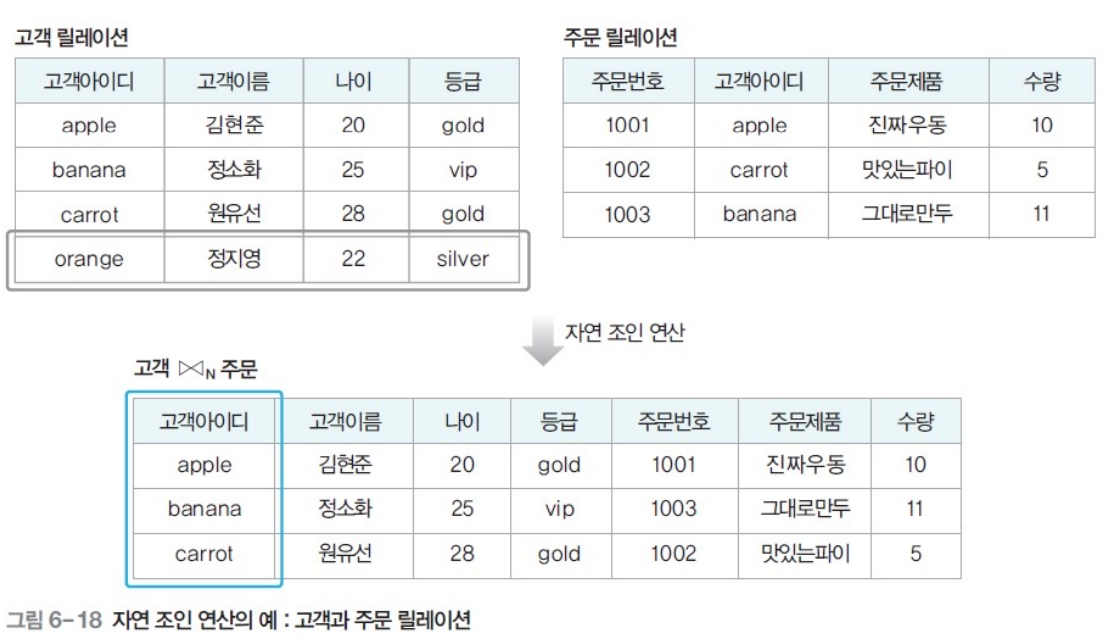
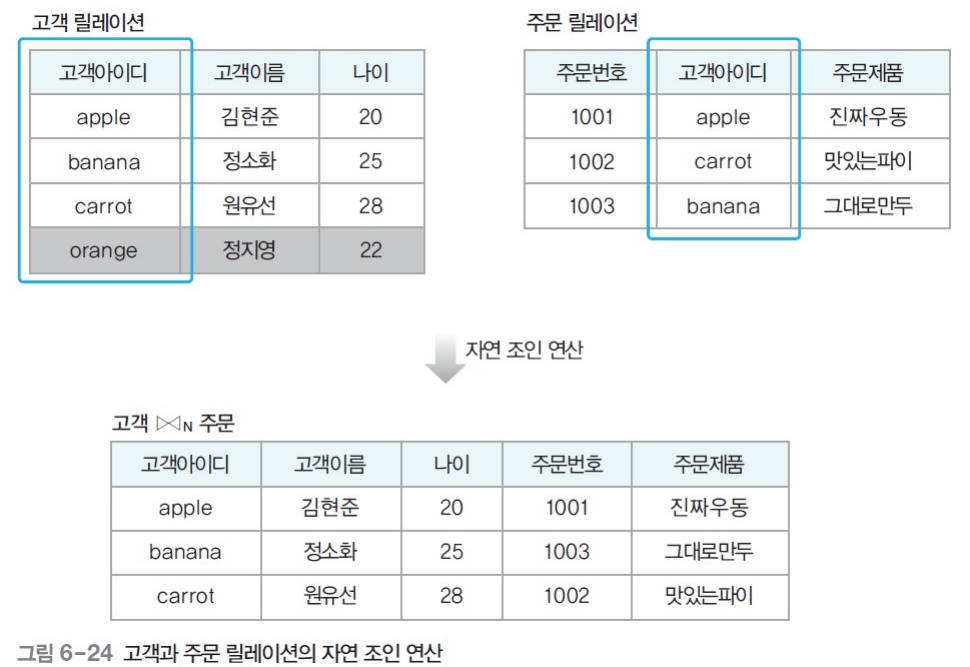
• 자연조인(natural join)
  • 동등 조인의 결과 릴레이션에서 조인 속성이 한 번만 나타나게 하는 연산
  • 표현법 : 릴레이션1 ⋈N 릴레이션2

 

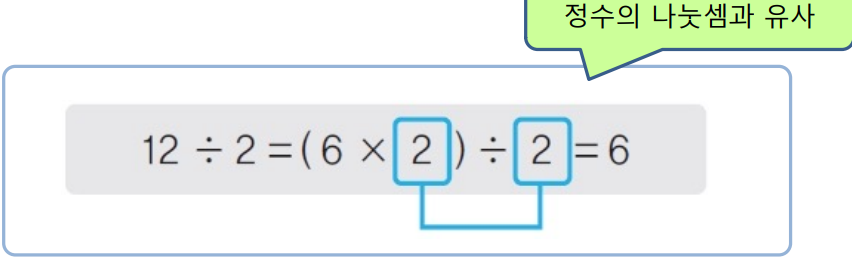
순수 관계 연산자 - 디비전(division)

• 표현법 : 릴레이션1 ÷ 릴레이션2 
• 릴레이션2의 모든 투플과 관련이 있는 릴레이션 1의 투플로 결과 릴레이션 구성
  • 단 릴레이션 1이 릴레이션 2의 모든 속성을 포함하고 있어야 연산 가능(도메인 같아야 한다는 의미)
    
    

 

여기에서 carrot과 바나나는 진짜우동이 없으니까 division항목에서 제외

orange는 주문내역이 없으므로 join에 포함되지 않는다.

 

확장된 관계 대수 연산자

• 기본 연산자들을 확장한 연산자들이 제안
  • ex) 자연조인 연산을 확장한 세미조인과 외부조인

 

 

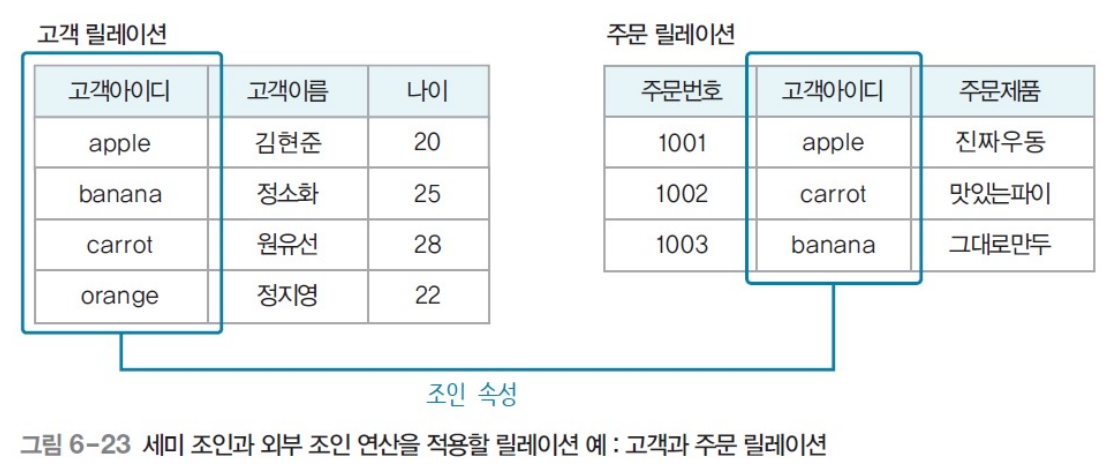
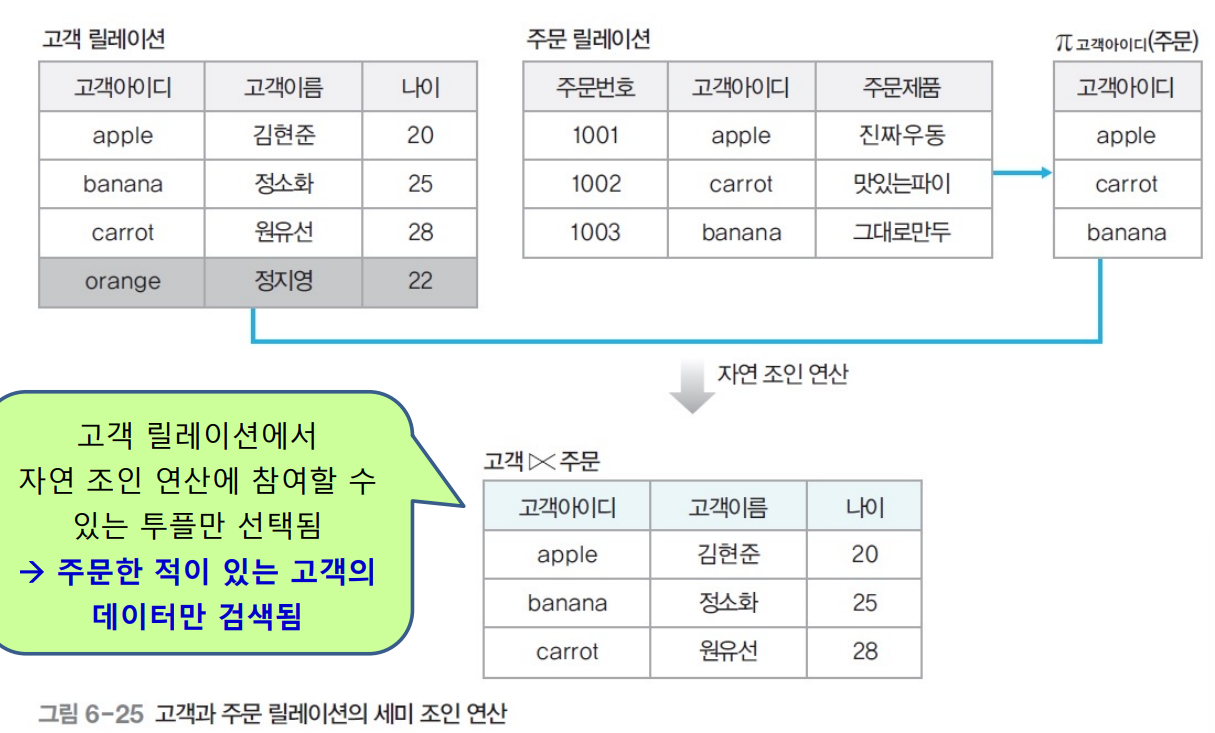
확장된 관계대수 연산자 - 세미 조인(semi-join)

• 조인 속성으로 프로젝트 연산을 수행한 릴레이션을 이용하는 조인
  • 표현법 : 릴레이션1 ⋉ 릴레이션2
• 릴레이션2를 조인속성으로 프로젝트 연산한 후, 릴레이션1에 자연조인하여 결과 릴레이션 구성
• 불필요한 속성 미리 제거 -> 조인 연산 비용 줄일 수 있다.
  • 교환적 특징이 없음  :  R ⋉ S ≠ S ⋉ R

 

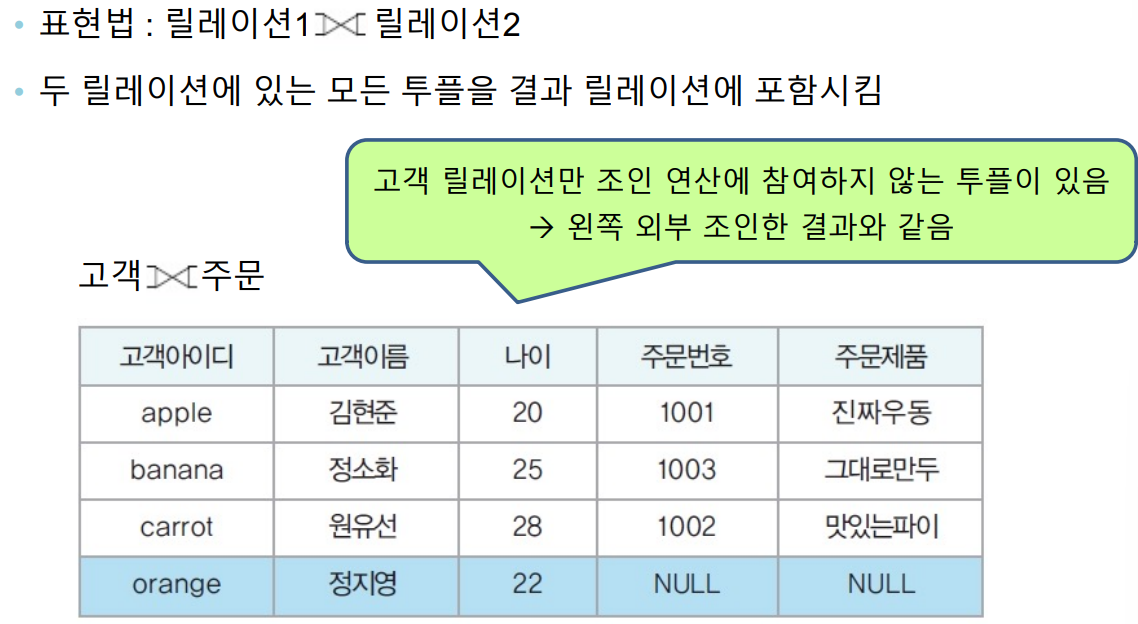
확장된 관계대수 연산자 - 외부 조인(outer-join)

• 자연조인연산에서 제외되는 투플도 결과 릴레이션에 포함시키는 조인
  • 결과 릴레이션에서 속성값이 없는 경우 : 널값으로 처리
• 분류
  • 왼쪽(left) 외부조인  / 오른쪽(right)외부조인 / 완전(full)외부조인
  • 모든 투플을 결과 릴레이션으로 가져오는 릴레이션이 무엇이냐에 따라 분류
    • 자연조인연산에서 제외되는 투플도 포함
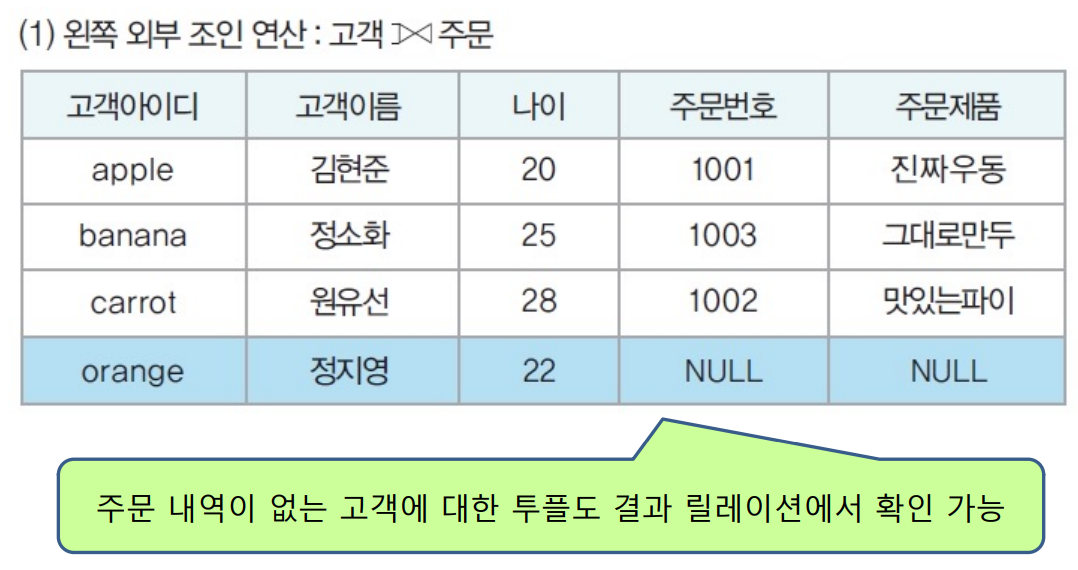
  • 왼쪽외부조인

왼쪽에 있는 릴레이션1에 존재하는 모든 투플을 결과 릴레이션에 포함

 

 

 

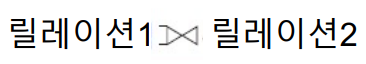
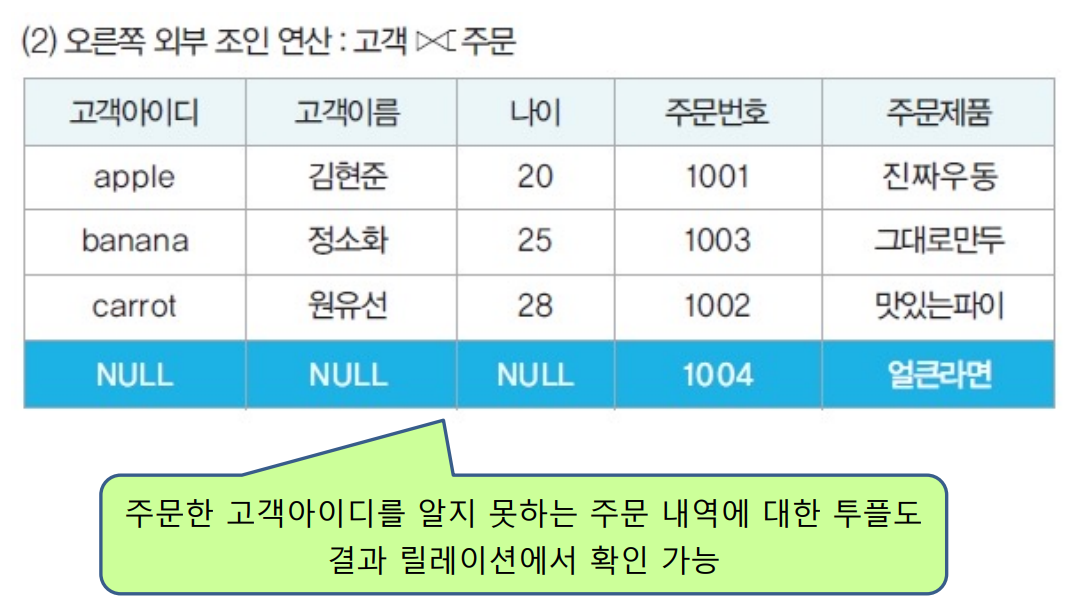
오른쪽 외부조인

 

 

완전 외부조인

 

 

<주문한 고객아이디는 모르는 새로운 주문내역투플이 주문 릴레이션에 추가된 상황>

 

 

03. 관계해석

관계 해석(relational calculus)

• 처리를 원하는 데이터가 무엇인지만 기술하는 언어
  • 비절차언어(nonprocedural language)
• 수학의 프레디킷 해셕(predicate calculus)에 기반
• 기능과 표현력 측면에서 관계 대수와 동등한 능력 지님
• 분류
  • 투플 관계 해석(tuple relation calculus)
  • 도메인 관계 해석(domain relational calculus)