hyejun CSlog

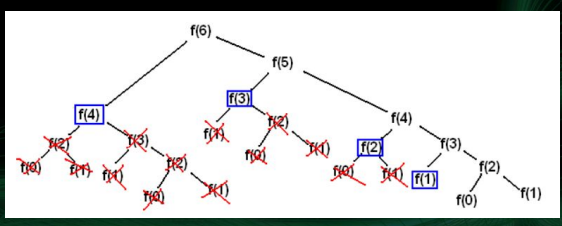
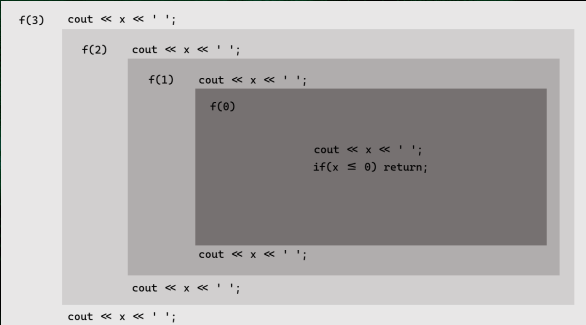
그리디욕심쟁이 방법 탐욕적 방법, 탐욕 알고리즘 등으로 불린다.우리가 원하는 답을 여러개의 조각으로 쪼개고, 각 단계마다 답의 한 부분을 만들어간다.모든 단계의 선택지를 고려해보지는 않는다.각 단계마다 지금 당장 좋은 근시안적 방법을 선택한다.계산속도가 빠르다.-> 많은 경우 최적해를 찾지 못한다. 특정 조건 하에서만 적용가능사용조건시간적, 공간적 제약으로 최적해를 구하지 못해, 근사해를 구해야 하는 문제 (대개 출제 x)탐욕법을 사용해도 항상 최적해를 구할 수 있는 문제탐욕선택속성 : 탐욕적으로 선택하더라도 문제의 최적해가 보장될 때(손해 x)최적 부분 구조 : 부분 문제의 최적해가 전체 문제의 최적해로 확장될 수 있을 때알고리즘의 정당성을 증명하는 과정 연습

5.1 상속의 개념 5.2 클래스 상속과 객체 자바의 상속선언extends 키워드 사용하여 상속선언상속 부모클래스 : 슈퍼클래스, 상속 자식클래스 : 서브클래스서브클래스는 슈퍼클래스의 private 멤버 외 모든 멤버에 접근할 수 있다.자바 상속의 특징클래스 다중상속 x (C++과 달리). 그러나 인터페이스는 다중상속 가능자바의 모든 클래스는 자바에서 제공하는 Object 클래스를 자동으로 상속받도록 컴파일된다. 5.3 protected 접근 지정자바의 접근 지정자 : private, public, protected, 디폴트 >>모든 멤버는 이 중 하나로 반드시 지정되어야 함.디폴트 접근 지정: 접근 지정자가 선언되어 있지 않을 때protected 멤버슈퍼클래스의 protected 멤버에 접근 가능한 경..

브루트포스 무차별 대입, 완전 탐색해답을 찾기 위해 가능한 모든 경우의 수를 찾는 기법시간복잡도는 입력크기에 비례간단하지만 매우 느림 BUT 떠올리기 가장 쉬운 기법 -> 문제를 풀 때 가장 먼저 고려해야 한다.입력범위와 시간복잡도를 잘 고려 분해합n의 분해합 = n과 n을 이루는 각 자리수의 합n의 생성자 = 분해합이 n인 어떤 자연수 m 비트마스킹비트 필드 각각을 하나의 원소처럼 사용하는 기법 C++ 에서 int는 32비트의 공간을 사용 -> int 한 개로 32개의 원소 저장 가능산술 연산보다 빠른 연산 수행가능1개의 int만으로 32개의 원소를 저장하는 효과효율적 메모리사용DP, 백트래킹 등 방문 여부를 저장해야 하는 알고리즘에 사용  비트연산자AND(&) : int ans = a & b;1100..

정수론이란?각종 수의 성질을 다룬다.약수 배수 최대공약수 최소공배수 소수 판결최대공약수소인수분해 이용 - 두 수 중 작은 수 기준으로 돌리면서 가장 큰 공통 약수 구하기구현 까다로움, 시간복잡도 O(n)유클리드 호제법: 시간복잡도 O(log(n))기본 원리A와 B의 최대공약수 = A-B 와 B의 최대공약수A = a*GB = b*G(a와 b는 서로소)A - B = a*G-b*G = (a-b)*G(a-b)와 b 또한 서로소 -> A-B 와 B의 최대공약수도 G이미 gcd⁡(a,b)=1 이므로, 어떤 정수 x,y 가 존재해서 ax+by=1을 만족시킨다. 그럼 (a−b)x+by=1도 만족. 어떤 정수 조합으로 1을 만들 수 있으니까 gcd(a−b,b)=1 이 된다.GCD(A,B) = GCD(A-B,B) -> A..

스택(Stack)LIFO(last in first out)자료의 맨 끝 위치에서만 모든 연산이 이루어진다.모든 연산에 대한 시간복잡도는 O(1)연산이 이루어지는 위치 : top, 삽입: push, 삭제: pop std::stackpush(element): top에 원소 추가pop(): top에 있는 원소 삭제top(): top에 있는 원소 반환empty(): 스택이 비어있는지 확인(비어있으면 true)size(): 스택 사이즈 반환* 파이썬은 ?따로 Stack 자료구조 제공 x. 이미 리스트에 모두 구현돼있다.list()stack = list()일 때...stack.append(element): top에 원소 추가stack.pop(): top에 있는 원소를 반환하고 삭제stack[-1]: top에 있는 ..

dynamic programming: 큰 문제를 부분문제로 쪼개어 푸는데, 여러 번 나오는 부분문제를 기억해서 최적화하는 기법 메모이제이션피보나치 수열: 단지 이미 계산한 값을 들고있는 것으로 호출의 양을 엄청나게 줄이는 것을 알 수 있다.dp - 메모이제이션 : 여러 번 나오는 부분 문제를 기억한다.사용법값을 저장해둘 테이블 만들기테이블을 식별할 수 있는 값으로 초기화해두기;내가 지금 풀어야 하는 문제의 답이 테이블에 존재하면 사용하기dp - 분할정복 : 문제를 바로 해결 가능하면 해결함. 지금 바로 해결 불가하면 문제를 잘게 쪼갠 후 조립문제 정의부분문제 정의내가 정의한 부분문제로 주어진 문제를 해결 가능한지 보이기내가 정의한 부분문제를 해결 가능한지 보이기

그래프: 정점의 집합과 간선의 집합으로 정의되는 이산수학의 추상적 구조정점: 어떠한 상태 or 위치 표현간선: 정점 사이의 관계나 연결성 표현ex) 지하철 노선도그래프의 종류모든 간선이 방향이 정해져 있지 않은 그래프하나의 간선으로 양방향으로 이동 가능방향이 정해져 있는 간선이 있는 그래프양방향 간선도 사실 방향이 있는 간선 두 개로 나눠서 생각해볼 수 있음간선에 가중치가 있는 그래프가중치: 간선 이용하는 비용일상예시: 지도 상의 여러 위치를 정점으로, 정점들 사이의 경로를 간선으로 잡으면 경로의 소요시간을 가중치로 모델링 가능같은 집합의 두 정점이 간선으로 이어지지 않게끔 정점들을 두 집합으로 나눌 수 있는 그래프초록색 정점들을 하나의 집합으로 묶고 회색 정점들을 하나의 집합으로 묶을 수 있다.판별법정..

1. 재귀함수함수 안에서 함수 호출 가능. 자기 자신도 호출 가능 >> 재귀함수void f(int x){ // x=3 cout 위는 재귀함수의 예시. 실행과정을 따라가보면 이상한 점 발견 ! x= 3에서 시작한다고 가정재귀적으로 f(3)이 호출된 후 f(2)가 호출된 후 f(1)이 호출된 후,,, 함수가 종료되지 않음!따라서 재귀함수는 종료조건 또는 기저조건을 설정하는 것이 중요void f(int x){ // x=3 cout xvoid f(int x){ if(x두 예시를 합친 예시와 호출과정을 시각화한 그림. 재귀호출이 몇 번 중첩돼 있는지를 재귀깊이라 부르기도 한다.void f(int x){ cout   백트래킹재귀적으로 모든 경우의 수를 탐색하는 문제. 일반적으로 모든 경우의 수를 구하거나 이에 대해..

1. bruteforce(무차별 대입공격)모든 경우에 대하여 조건에 맞는지 검사하는 방법더보기다음 연립방정식에서 x와 y의 값을 계산하시오.   ax+by=c dx+ey=f 각 칸에는 -999 이상 999 이하의 정수만 입력할 수 있다.식정리: ax + by = c , dx + ey = f , x = (c-by)/a로 구해두고 d(c-by)/a+ey = f , d(c-by) + ae , y = af y(ae-bd) = af-dc , y = (af-dc)/(ae-bd) 로 구할 수 있나?! --> 오류발생 !!y = (af-dc)/(ae-bd) 에서 ae-bd=0이라면 0으로 나누는 오류 발생, 이를 케어해줬다 해도 나누는 연산으로 인해 각종 억까 발생가능x와 y의 범위가 [-999,999]인 정수이므로 ..

prefix sum(누적합)배열에서 각 위치까지의 합을 미리 계산하는 기법f(i) = 구간 [1,i]의 원소를 합친 값알아볼 것우리가 원하는 것을 구할 수 있는가이걸 구하는 것은 효율적인가f(1)부터 f(n)까지 모두 구했다고 가정 -> 문제에서 요구하는 구간[i,j]에 속하는 원소들의 합을 구해야 함.f(j)-f(i-1)로 구할 수 있음f(1)부터 f(n)까지 구하려면 1+2+...+n번 연산해야돼서 나이브(별 다른 처리를 하지 않다)하게 구하면 O(N^2) but 최적화를 통해 O(N)으로 만들기f(i)=구간 [1,i]의 원소의 합 ---> f(i-1)=구간 [1,i-1]의 원소 합.f(i-1)을 안다면 f(i)=f(i-1)+A[i]로 O(1)만에 구할 수 있다.f(1)=A[1]이므로 이도 O(1)이..