8.1 트리의 개념
- 트리: 계층적인 구조를 나타내는 자료구조(계층적인 구조)<->선형자료구조(리스트, 스택, 큐), 한 개 이상의 노드로 이루어진 유한 집합

- 노드(node): 트리의 구성요소에 해당하는 A, B, C, D, E , F, G, H, J
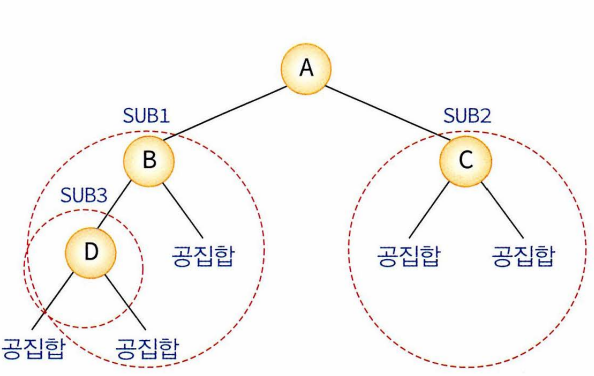
- A: 루트/ 서브트리에서는 B,C,D가 루트
- 연결선: 간선(edge)
- A는 B의 부모노드, B는 A의 자식노드, B와C와D는 형제관계
- 조상노드: 임의의 노드 상위에 연결되어 뻗쳐나간 모든 노드
- 후손노드: 임의의 노드 하위로 연결되어 뻗쳐나간 모든 노드
- 단말노드: 자식노드가 없는 노드 <->비단말노드
- 노드 차수: 어떤 노드가 갖고 있는 자식노드의 개수
- 트리 차수: 트리가 갖고있는 노드의 차수 중 가장 큰 값
- 트리 레벨: 트리의 각층에 번호 매기기(루트의 레벨이 1, 한 층씩 내려갈수록 1씩증가
- 트리높이: 트리가 갖고 있는 최대 레벨
- 트리들의 집합: forest
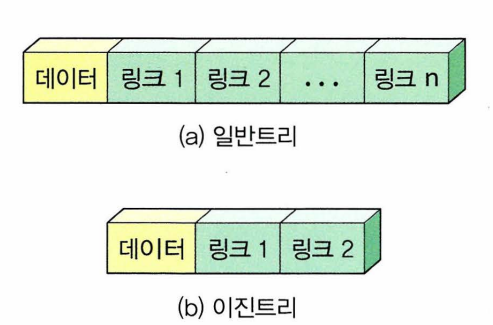
링크> 트리를 프로그램 안에서 표현하는 가장 일반적인 방법
: 각 노드가 데이터필드와 링크필드(자식노드) 갖게 함 > 문제점: 노드의 크기 고정x
8.2 이진트리 소개
- 이진트리: 모든 노드가 2개의 서브트리 갖고있는 트리(서브트리 공집합일 수 있음)> 모든 노드의 차수가 2 이하 / 서브트리간 순서 존재> 왼쪽 오른쪽 서브트리 구별
- 성질: n개의 노드가진 이진트리는 정확히 n-1개 간선 가짐
- 높이가 h인 이진트리는 최소 h개의 노드 가지며 최대 2^h-1개 노드 가짐 >>전체 노드 개수: 2^h-1

- n개의 노드 가지는 이진트리 높이는 최대 n, 최소 [ log2(n+ 1)] / n>= h>= log2(n+ 1) / 높이 h의 이진트리가 가질 수 있는 노드의 최대값: 2^h-1 / 2^h-1>=n
<이진트리의 분류>
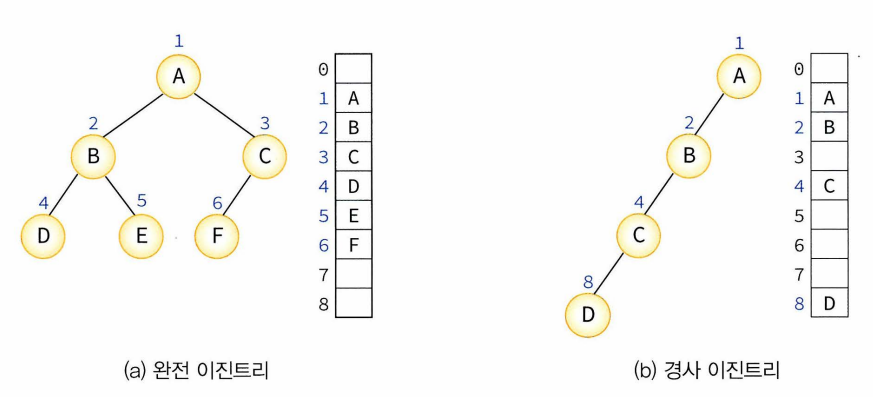
-포화이진트리(full binary tree): 각 레벨에 노드 꽉 차있음, 정확하게 2^k-1개 노드 가짐
노드에 번호 부여하는 방법: 레벨 단위로 왼>오, 루트부터 시작
-완전이진트리(complete binary tree): 높이가 k일 때 레벨 1부터 k-1까지는 노드가 모두 채워져 있고 마지막 레벨 k에서ㅡㄴ 왼쪽부터 오른쪽으로 노드가 순서대로 채워져 있음(마지막레벨에서 노드 꽉 차있지 않아도 되지만 중간에 빈 곳 있으면 안됨.
8.3 이진트리의 표현
-배열: 주로 포화, 완전이진트리에 사용 but 일반이진트리에도 사용가능-공간낭비 심함. *배열은 0이 아닌 1부터 시작
ㄴ배열표현법에서 부모와 자식 인덱스 관계: 노드 i의 부모 노드 인덱스=i/2, 노드 왼쪽 자식노드 인덱스=2i, 노드 i 오른쪽 자식 인덱스=2i+1
-링크 표현법: 트리에서의 노드가 구조체로 표현, 각 노드가 하나의 데이터필드와 왼 오 포인터 필드 갖고있고 이걸로 부모노드와 자식노드 연결. 구조체를 이용하여 노드 구조 정의, 링크는 포인터 개념 이용해서 정의, 노드들은 모두 동적 메모리 할당으로 생성, 연결리스트처럼 포인터만 있으면 트리 안



연결리스트와 아주 유사.(1차원<->2차원)
8.4 이진트리의 순회
- 이진트리 순회: 이진트리에 속하는 모든 노드를 한번씩 방문> 노드가 갖고 있는 데이터를 목적에 맞게 처리
ㄴ선형구조와 달리 여러가지 순서로 노드가 갖고 있는 자료에 접근가능
순회알고리즘은 순환 이용(문제의 구조는 같고 크기만 작아지는 경우)
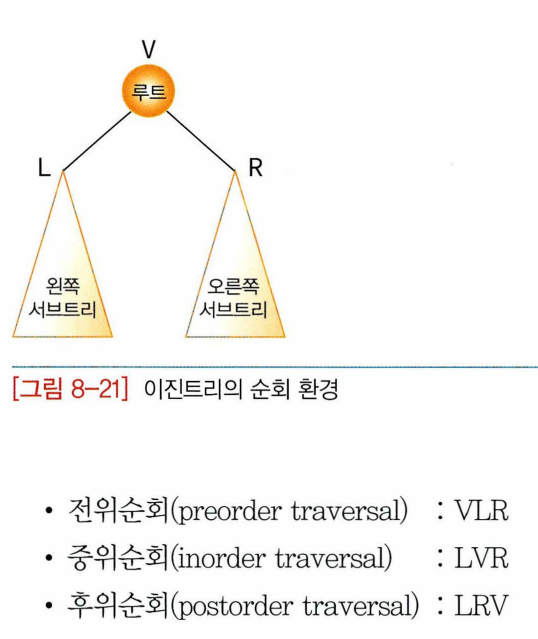
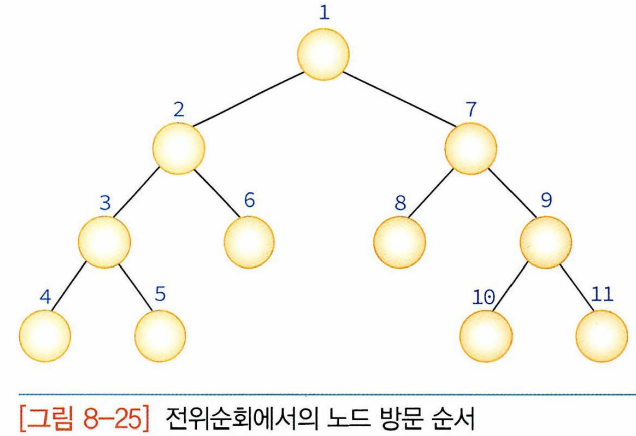
전위:
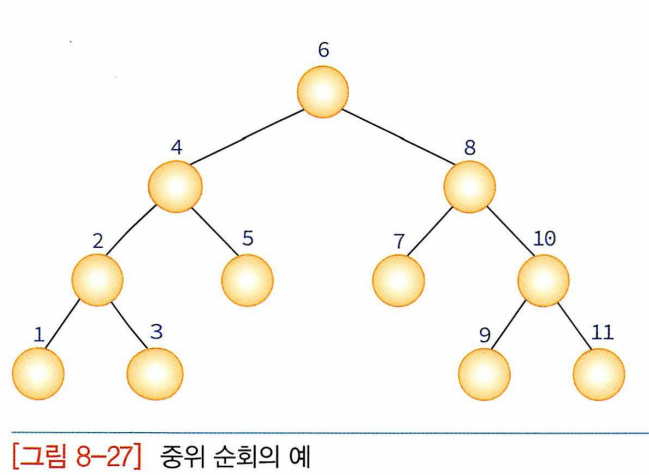
중위:
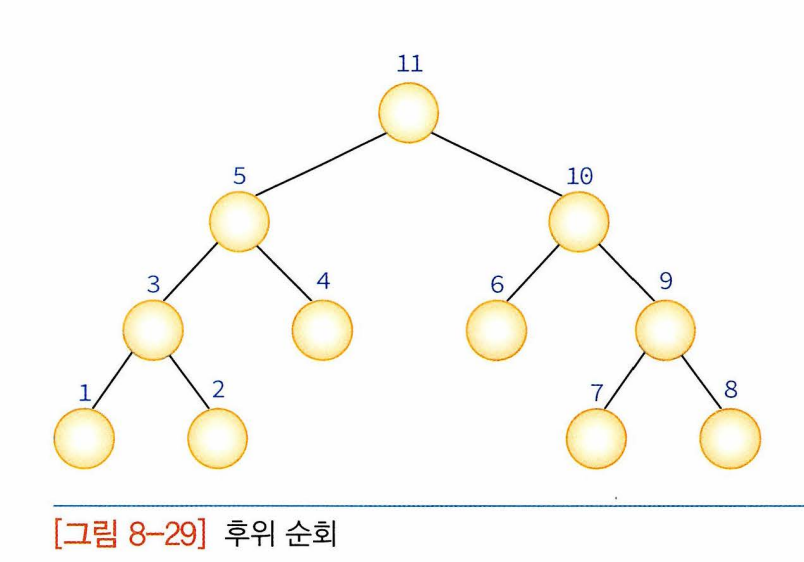
후위:
8.5 반복적 순회
- 표준적 방법: 순회를 순환호출 이용하여 구현
-반복 이용하여 트리 순회 가능 > 스택에 자식 노드들을 저장하고 꺼내면서 순회
8.6 레벨 순회
-각 노드를 레벨 순으로 검사, 큐 순회 사용
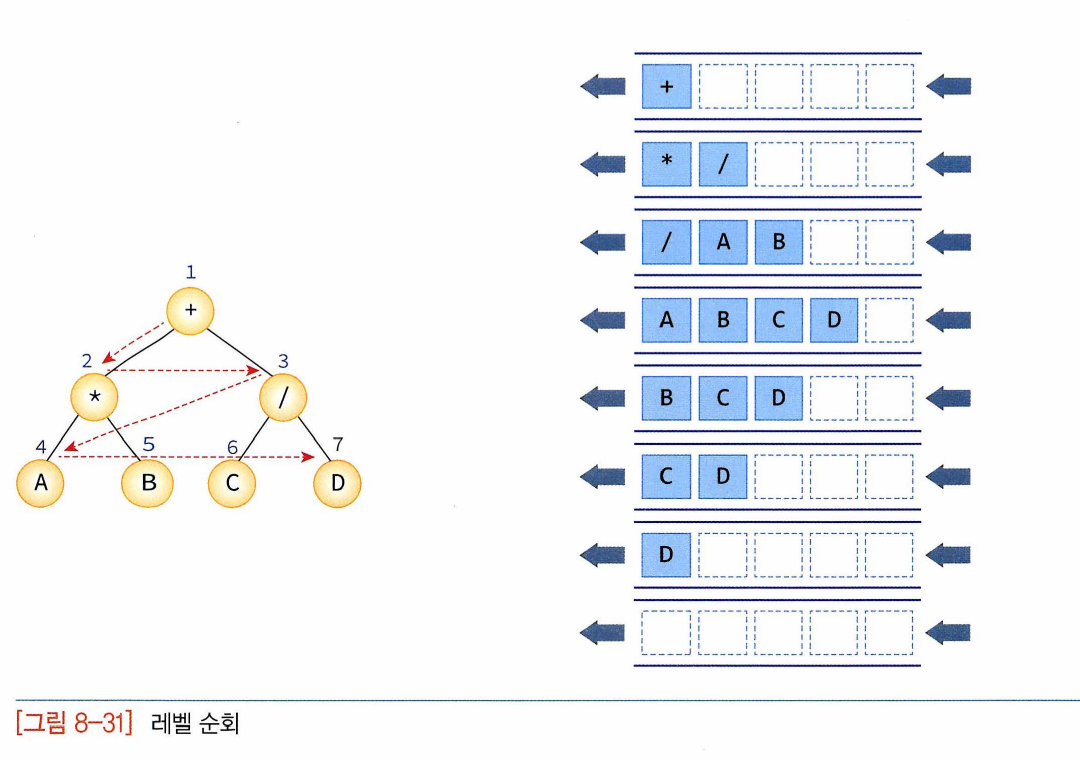
큐에 노드가 하나라도 있으면 계속 반복
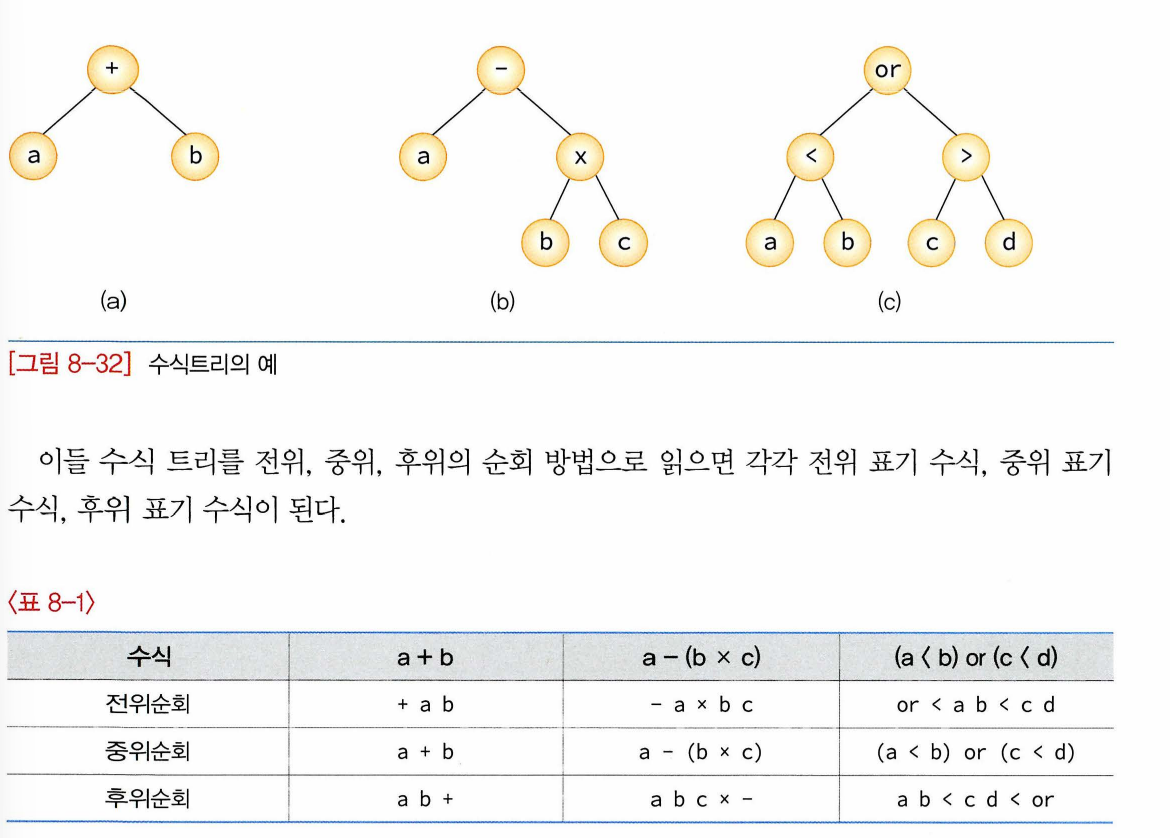
8.7 트리의 응용: 수식 트리 처리
-수식 트리를 처리하는 데 이진트리 사용 가능:
8.8 트리의 응용: 디렉토리 용량 계산
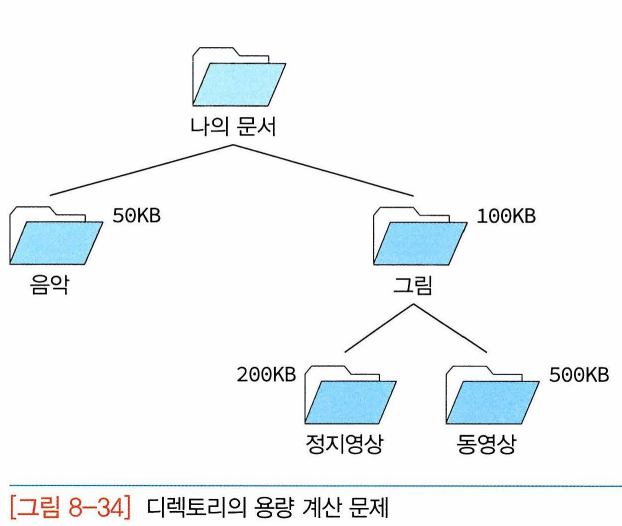
-하나의 디렉토리 안에 다른 디렉토리 있을 수 있으므로 먼저 서브 디렉토리 용량 모두 계산한 후에 루트 디렉토리의 용량 계산. > 후위순회 사용
8.10 스레드 이진 트리
-이진트리가 사용하는 순환호출은 함수 호출해야 해서 비효율적일 수 있다.
-이진트리 순회도 노드개수 많아지고 트리 높이 커지면 상당히 비효율적일 수 있다.
-순회를 순환호출 없이(스택의 도움 없이) 할 수 있는 방법?
ㄴ NULL 링크 사용 : NULL링크에 중위순회 시 선행노드인 중위 선행자 OR 중위 순회시 후속 노드인 중위 후속자 를 저장시켜 놓은 트리(스레드 이진 트리) 사용 > 스레드(실)을 이용하여 노드들을 순회 순서대로 연결
ㄴ스레드 트리는 순회 빠르게 하는 장점에 더불어 스레드 설정 위해 삽입이나 삭제함수가 많은 일을 해야 한다는 단점이 있다.
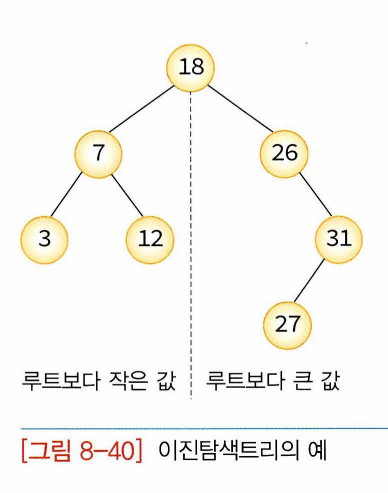
8.11 이진탐색트리
-탐색: 레코드(record)의 집합에서 특정한 레코드를 찾아내는 작업.
-이진탐색트리: 이진트리 기반의 탐색을 위한 자료구조


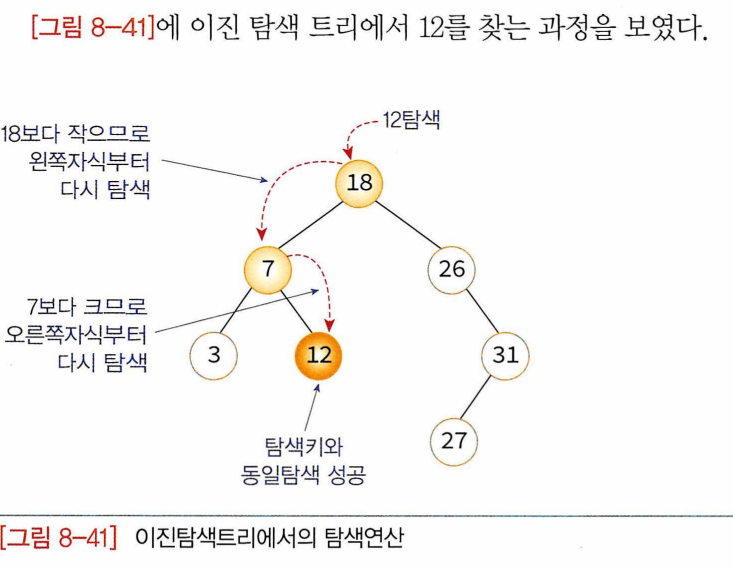
-순환적인 탐색연산:
-이진탐색트리에서 삽입 연산: 먼저 탐색 수행> 탐색이 실패한 위치에 특정 숫자 삽입.

-이진탐색트리에서 삭제 연산: 먼저 노드 탐색> 삭제하려는 키값 찾기
1. 삭제하려는 노드가 단말노드일 경우
>>단말노드의 부모노드를 찾아서 부모노드안의 링크필드 NULL로 만들어서 연결을 끊는다.

2. 삭제하려는 노드가 하나의 서브트리만 갖고 있는 경우
>> 자기 노드는 삭제하고 서브트리를 자기 노드의 부모노드에 붙여주면 된다.

3. 삭제하려는 노드가 두개의 서브트리를 갖고 있는 경우
>> 서브트리에 있는 어떤 노드를 삭제 위치로 가져올 것이냐가 문제. (이진트리 조건을 만족해야 함)
ㄴ 삭제되는 노드와 가장 값이 비슷한 노드로 대체해야 한다. 그럼 그 노드는 어디에 있느냐? 왼쪽 서브트리에서 가장 큰 값이나 오른쪽 서브트리에서 가장 작은 값이 삭제되는 노드와 가장 가깝다. (이진트리 중위순회했을때의 선행노드와 후속노드)

-이진탐색트리의 분석
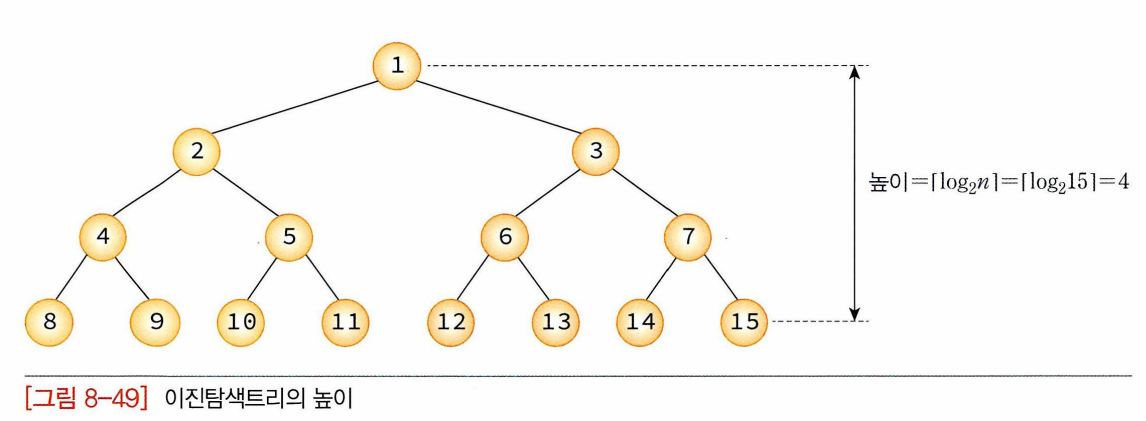
- 탐색, 삽입, 삭제 연산의 시간 복잡도: 트리의 높이가 h일 때 O(h).

이므로 이진탐색트리 연산의 평
- 트리의 높이가 h일 때 O(h). n개n개의 노드를 갖는 이진탐색트리의 일반적 높이
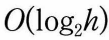
이진탐색트리연산의 평균적인 경우 시간 복잡도(좌우의 서브 트리가 균형 이룰 경우)
*최악의 경우: 한쪽으로 치우치는 경사트리: 트리 높이 n, 연산 시간 복잡도: O(n)
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] chap10. 그래프 I (4) | 2024.11.05 |
|---|---|
| [자료구조] chap9. 우선순위 큐 (0) | 2024.10.22 |
| [자료구조] chap7. 연결리스트 II (0) | 2024.10.21 |
| [자료구조] chap6. 연결리스트 I (1) | 2024.10.18 |
| [자료구조] chap5. 큐 (0) | 2024.10.17 |