10.1 그래프란?
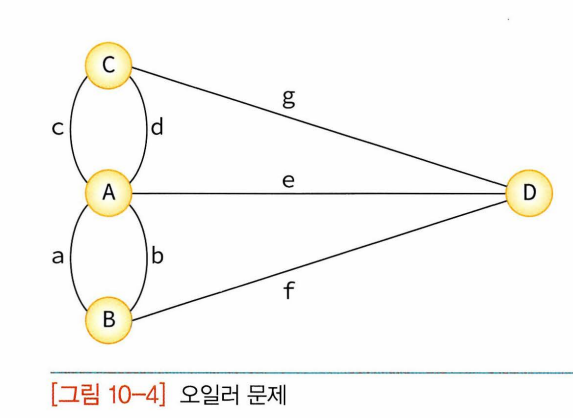
- 그래프: 객체사이 연결관계 표현하는 자료구조 (ex. 지하철노선도), 선형리스트나 트리(트리도 그래프의 종류이긴 함)의 구조보다 복잡. 인접행렬이나 인접리스트로 메모리에 표현되고 처리될 수 있음.
10.2 그래프의 정의와 용어
- 정점과 간선들의 유한집합
- 수학적으로는 G=(V,E)와 같이 표시.
- V(G)는 그래프 G의 정점들의 집합, E(G)는 그래프 G의 간선들의 집합
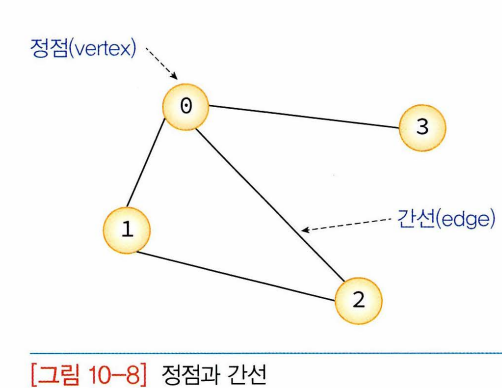
- 정점 vertex (=노드 node) : 여러가지 특성을 가질 수 있는 객체,
- 간선 edge (링크 link): 이러한 정점들 간 관계

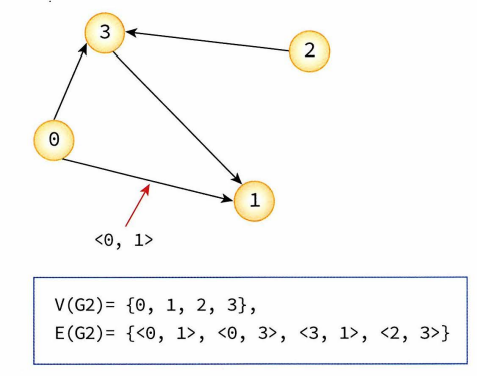
- 무방향 그래프와 방향 그래프
- 무방향그래프 : 간선을 통해서 양방향으로 갈 수 있음을 나타냄, (A,B)=(B,A)

- 방향그래프: 간선에 방향성 존재. 간선을 통하여 한쪽 방향으로만 갈 수 있음을 나타냄, <A,B>!=<B,A>
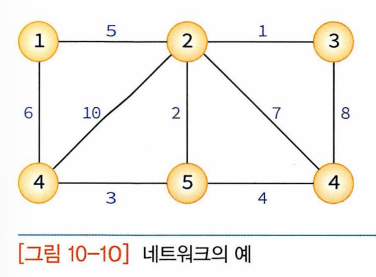
- 네트워크(가중치 그래프)
- 간선에 비용이나 가중치 할당(간선으로 두 정점간 연결 유무뿐만 아니라 연결 강도까지 나타낼 수 있음)
- 부분그래프: 어떤 그래프의 정점의 일부와 간선의 일부로 이루어진 그래프
- 그래프 G의 부분 그래프 S는 다음과 같은 수식 만족시킴


- 정점의 차수
- 인접정점: 간선에 의해 직접 연결된 정점
- 무방향그래프에서 정점의 차수: 그 정점에 인접한 정점의 수
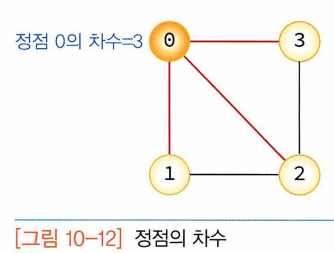
- 무방향그래프에서 모든 정점의 차수를 합하면 간선 수의 2배. 하나의 간선이 두 개의 정점에 인접.
- 방향그래프에서 외부에서 오는 간선의 개수: 진입차수, 외부로 향하는 간선의 개수: 진출차수
- 경로
- 무방향그래프에서 정점 s로부터 정점 e까지의 경로는 정점의 나열. 경로가 성립되려면 나열된 정점 간에는 반드시 간선 있어야 함.
- 단순경로: 경로 중 반복되는 간선 없을 경우
- 사이클: 단순 경로의 시작 정점과 종료 정점이 동일할 때
- 무방향그래프에서 정점 s로부터 정점 e까지의 경로는 정점의 나열. 경로가 성립되려면 나열된 정점 간에는 반드시 간선 있어야 함.
- 연결그래프
- 무방향그래프 G에 있는 모든 정점쌍에 대하여 항상 경로가 존재할 때 (그렇지 않은 그래프는 비연결그래프)
- 트리는 그래프의 특수한 형태, 사이클 갖지 않는 연결그래프
- 무방향그래프 G에 있는 모든 정점쌍에 대하여 항상 경로가 존재할 때 (그렇지 않은 그래프는 비연결그래프)

- 완전그래프 : 그래프에 속해있는 모든 정점이 서로 연결
- 무방향 완전 그래프의 정점 수: n, 하나의 정점은 n-1개의 다른 정점으로 연결, 간선의 수는 n*(n-1)/2
- 그래프 추상 데이터 타입

10.3 그래프의 표현 방법
- 인접 행렬 : 그래프 정점 수가 n이라면 n*n의 2차원 배열인 인접행렬 M의 각 원소를 아래 규칙에 의해 할당함으로써 그래프 메모리에 표현

- 그래프에서 자체 간선을 허용하지 않으므로 인접 행렬의 대각선 성분은 모두 0으로 표시.
- 무방향 그래프의 인접 행렬은 대칭행렬 - 무방향 그래프의 간선 (i,j)는 정점 i에서 j로의 연결+정점 j에서 i로의 연결 동시에 의미. >> 배열의 상위 삼각이나 하위 삼각만 저장하면 메모리 절약할 수 있음.
- but 방향그래프의 인접행렬은 일반적으로 대칭 x.

- n개의 정점을 갖는 그래프를 인접 행렬으로 표현하기 위해서는 간선의 수에 무관하게 항상 n^2개의 메모리공간 필요> 밀집그래프(a와 같이 그래프에 간선이 많이 존재)를 표현하는 경우에는 적합, 희소그래프 (b와 같이 그래프 내에 적은 숫자의 간선만을 가짐)에는 적합하지 않음.
- 인접행렬의 장점 : 두 정점을 연결하는 간선의 존재 여부를 O(1)시간 안에 즉시 알 수 있음. (정점 u, 정점 v를 연결하는 정점이 있는지 알려면 M[u][v]의 값을 조사하면 됨. )
- 정점의 차수 : 인접행렬의 행이나 열을 조사하면 알 수 있음 > O(n)의 연산에 의해 알 수 있음
- 그래프에 존재하는 모든 간선의 수 알아내려면 인접행렬 전체 조사해야 함> n^2번의 조사가 필요 > O(n^2)의 시간이 요구됨.
- 정점의 차수 : 인접행렬의 행이나 열을 조사하면 알 수 있음 > O(n)의 연산에 의해 알 수 있음
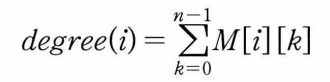
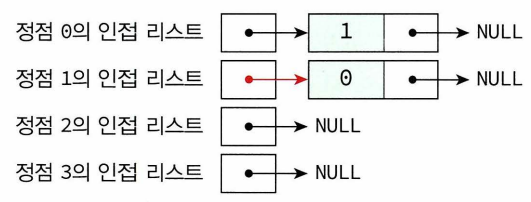
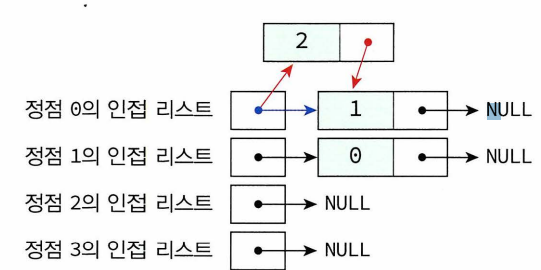
- 인접 리스트 : 각각의 정점에 인접한 정점들을 연결리스트로 표시하여 그래프 표현. 각 연결리스트 노드들은 인접 정점 저장, 각 연결리스트들은 헤더노드 갖고 있고 이 헤더노드들은 하나의 배열로 구성. 정점의 번호만 알면 이 번호를 배열의 인덱스로 하여 각 정점의 연결리스트에 쉽게 접근.
- 무방향그래프의 경우 정점 i와 정점 j를 연결하는 간선 (i,j)는 저점 i의 연결리스트에 인접정점 j로서 한 번, 정점 j의 연결리스트에 인접정점 i로 다시 한 번 표현.
- 인접리스트의 각각의 연결리스트에 정점이 입력되는 순서에 따라 연결리스트 내에서 정점들의 순서가 달라질 수 있음 > 그래프 표현의 일관성 유지 위해 인접리스트가 정점의 오름차순으로 연결된다고 가정.
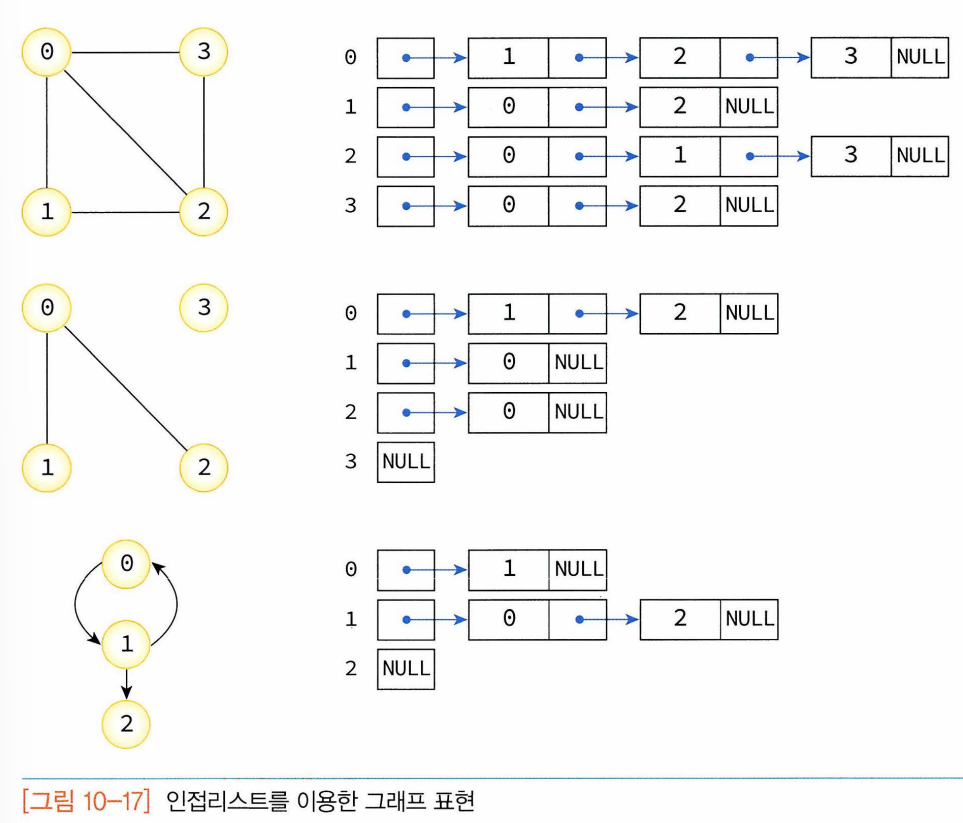
-> 정점의 수가 n개이고 간선의 수가 e개인 무방향 그래프를 표시하기 위해서는 n개의 연결리스트가 필요하고 n개의 헤더노드, 2e개의 노드가 필요. >> 인접행렬표현은 간선의 개수가 적은 희소그래프의 표현에 적합.
그래프에 간선 (i,j)의 존재 여부나 정점 i의 차수를 알기 위해서는 인접리스트에서의 정점 i의 연결리스트 탐색해야 함, 연결리스트에 있는 노드의 수(정점차수)만큼의 시간이 필요.
---> n개 정점과 e개 간선을 가진 그래프에서 전체 간선의 수 알아내려면 헤더노드 포함하여 모든 인접 리스트 조사해야 함 > O(n+e)의 연산 요구
10.4 그래프의 탐색
- 그래프 탐색 : 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것.
- ex 특정한 정점에서 다른 정점으로 갈 수 있는지 없는지를 탐색을 통해 알 수 있음.
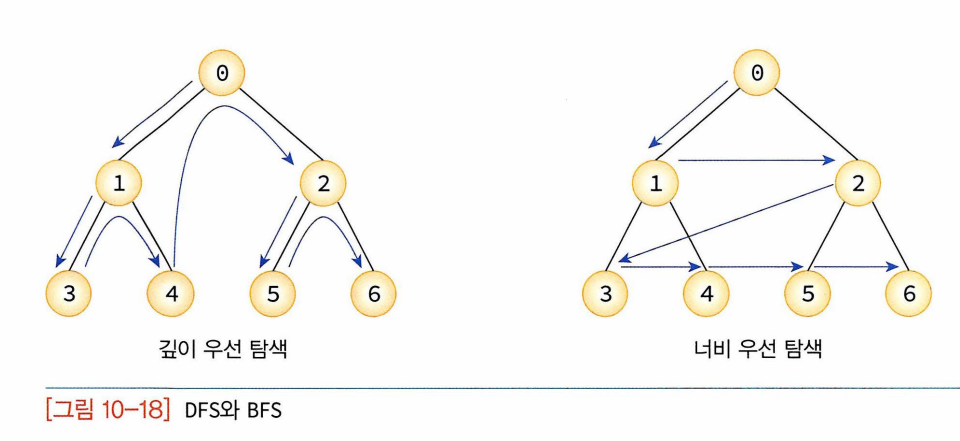
- 깊이 우선 탐색(DFS : depth first search) : ex 트리, 시작 정점에서 한 방향으로 계속 가다가 갈 수 없게되면 다시 가장 가까운 갈림길로 돌아와서 다른 방향으로 다시 탐색 진행
- 너비 우선 탐색(BFS : breath first search) : 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문.
10.5 깊이우선탐색
- 자기 자신을 다시 호출하는 순환 알고리즘 형태

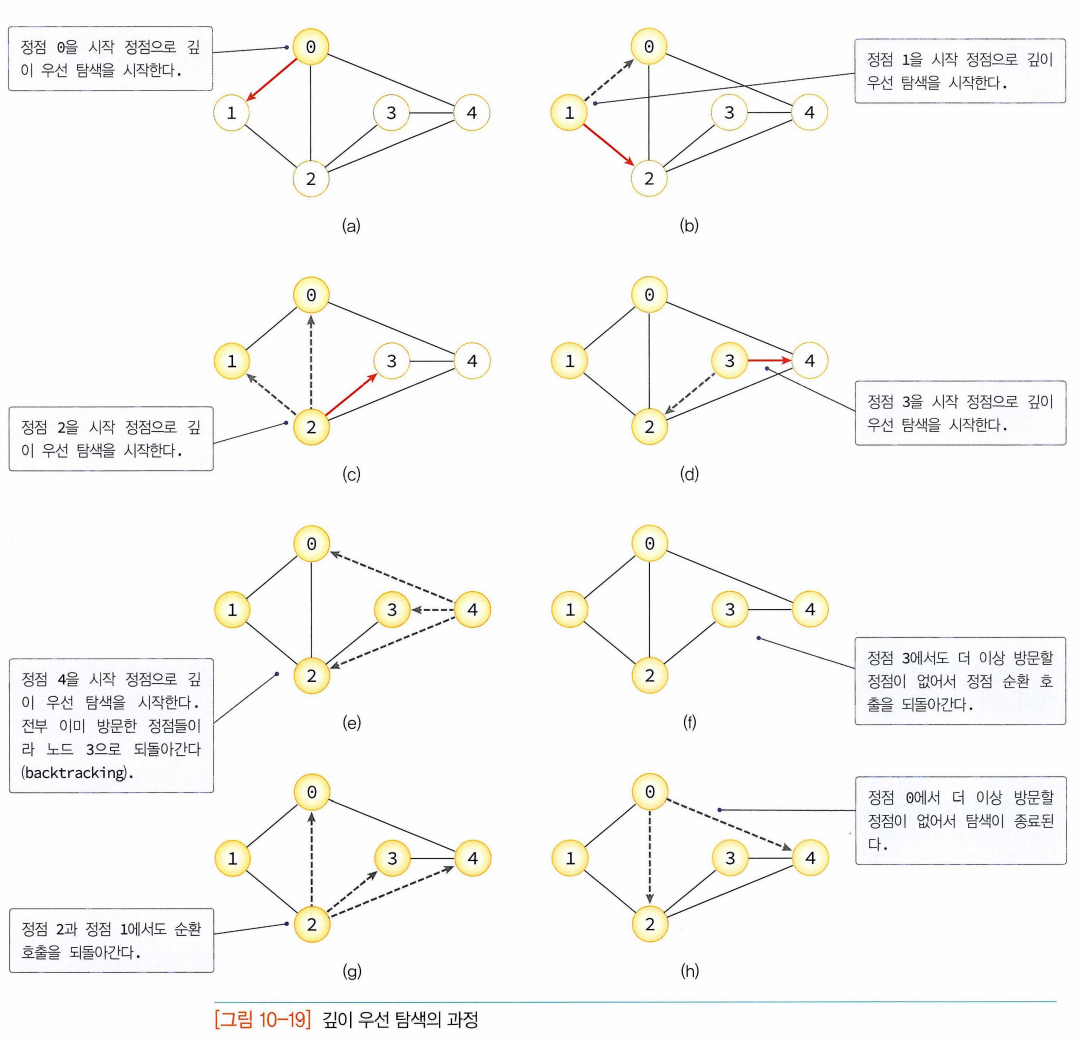
- 깊이우선탐색의 구현
- 순환호출 이용
- 명시적인 스택 사용하여 인접한 정점들을 스택에 저장했다가 다시 꺼내어 작업.
- 분석
- 그래프의 모든 간선을 조사, 정점의 수가 n, 간선의 수가 e인 그래프인 경우 시간복잡도
- 인접리스트로 표현-> O(n+e)
- 인접 행렬로 표시 -> O(n^2)
- 그래프의 모든 간선을 조사, 정점의 수가 n, 간선의 수가 e인 그래프인 경우 시간복잡도
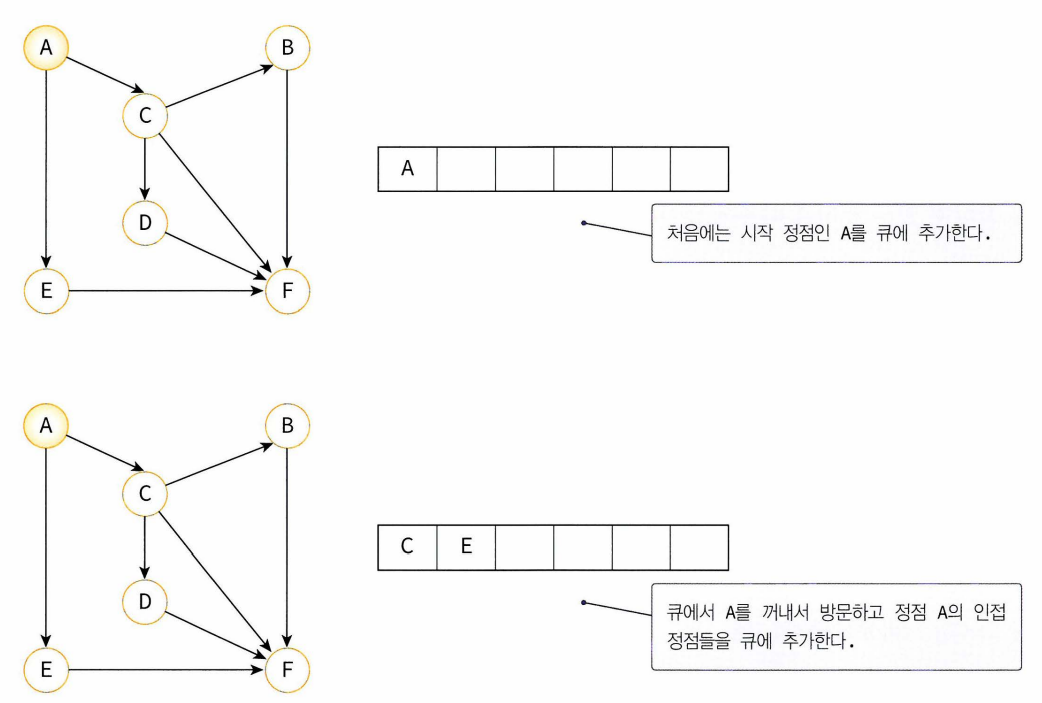
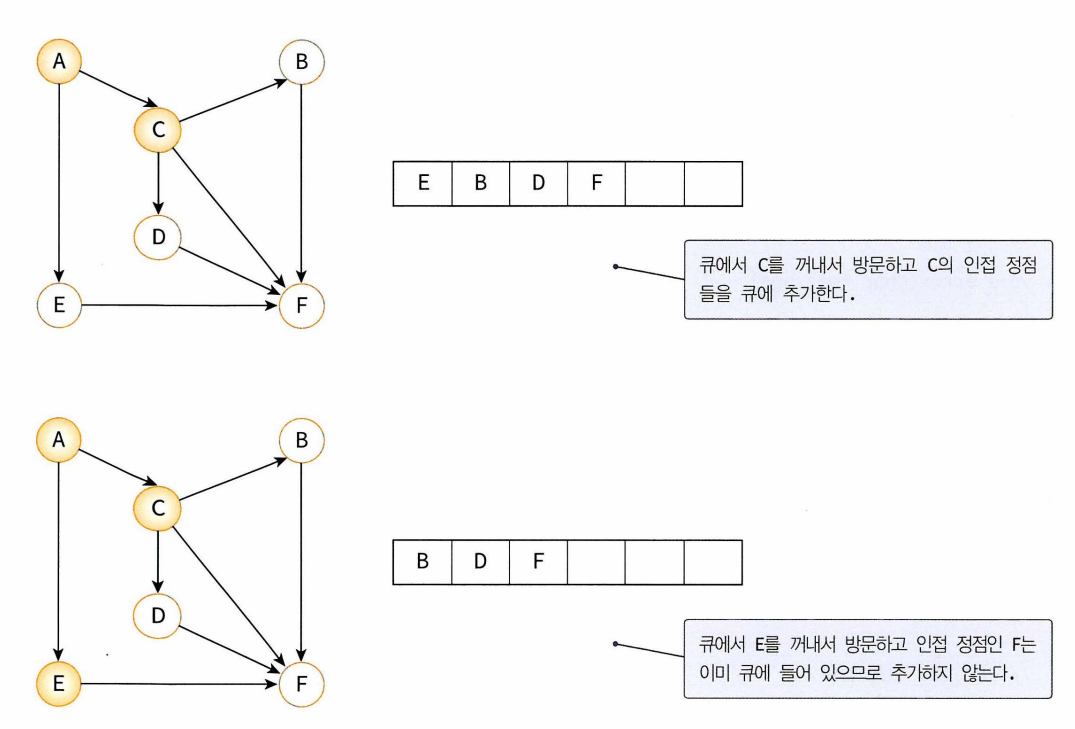
10.6 너비우선탐색
- 너비우선탐색(BFS : breath first search): 시작 정점으로부터 가까운 정점 먼저 방문하고 멀리 떨어져있는 정점 나중에 방문

- 가까운 거리에 있는 정점들을 차례로 저장한 후 꺼낼 수 있는 자료구조인 큐 필요.

'CS > 자료구조' 카테고리의 다른 글
| [자료구조] chap12. 정렬 (0) | 2024.11.19 |
|---|---|
| [자료구조] chap11. 그래프 II (1) | 2024.11.12 |
| [자료구조] chap9. 우선순위 큐 (0) | 2024.10.22 |
| [자료구조] chap8. 트리 (0) | 2024.10.22 |
| [자료구조] chap7. 연결리스트 II (0) | 2024.10.21 |