- 11.1 최소 비용 신장 트리
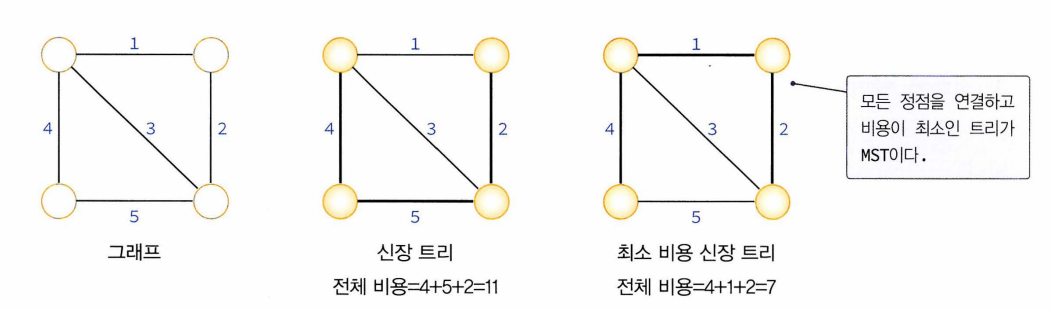
- 신장트리: 그래프내 모든 정점을 포함하는 트리
- 트리의 특수한 형태 : 모든 정점 연결, 사이클 포함 x
- 그래프에 있는 n개의 정점을 정확히 (n-1)개의 간선으로 연결. 하나의 그래프에는 많은 신장트리 존재.
- 깊이 우선이나 너비 우선탐색 때 사용한 간선들 표시하면 신장트리 만들 수 있음.
- 그래프의 최소연결부분 그래프(간선의 수가 가장 적음)
- n개의 정점 갖는 그래프는 최소 (n-1)개 간선 가져야 함,
- (n-1)의 간선으로 연결돼있으면 필연적으로 트리형태>신장트리
- 통신네트워크 구축에 많이 사용
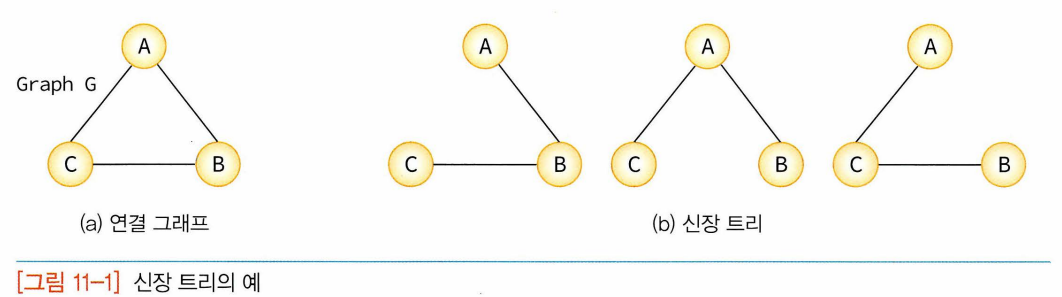

- 최소비용신장트리
- 네트워크에 있는 모든 정점들을 가장 적은 수의 간선과 비용으로 연결
- 신장트리 중 사용된 간선들의 가중치 합이 최소.
- 각 링크의 구축 비용은 똑같지 x -> 각 링크(간선)에 비용 붙여서 링크의 구축 비용까지 고려하여 최소비용의 신장 트리를 선택할 필요가 있음.
11.2 Kruskal의 MST 알고리즘
- 탐욕적인 방법 이용 : 선택할때마다 그 순간 가장 좋다고 생각되는 것을 선택
- 순간의 선택은 그 당시에 최적이지만 최적이라고 생각했던 지역적인 해답들을 모아서 최종적인 해답을 만들었다고 해서 그 해답이 반드시 전역적으로 최적이라는 보장 X -> 항상 최적의 해답을 주는지 검증해야 함.(Kruskal의 알고리즘은 최적의 해답 주는걸로 증명)
- 최소비용신장트리가 최소비용의 간선으로 구성됨과 동시에 사이클을 포함하지 않는다는 조건에 근거하여 각 단계에서 사이클을 이루지 않는 최소비용간선 선택 > 네트워크의 모든 정점 최소비용으로 연결하는 최적 해답 구할 수 있음.
- 알고리즘 : 먼저 그래프의 간선들을 가중치의 오름차순으로 정렬, 정렬된 간선들의 리스트에서 사이클을 형성하지 않는 간선 찾아서 현재의 최소비용신장트리의 집합에 추가. (사이클 형성하면 그 간선 제외.)

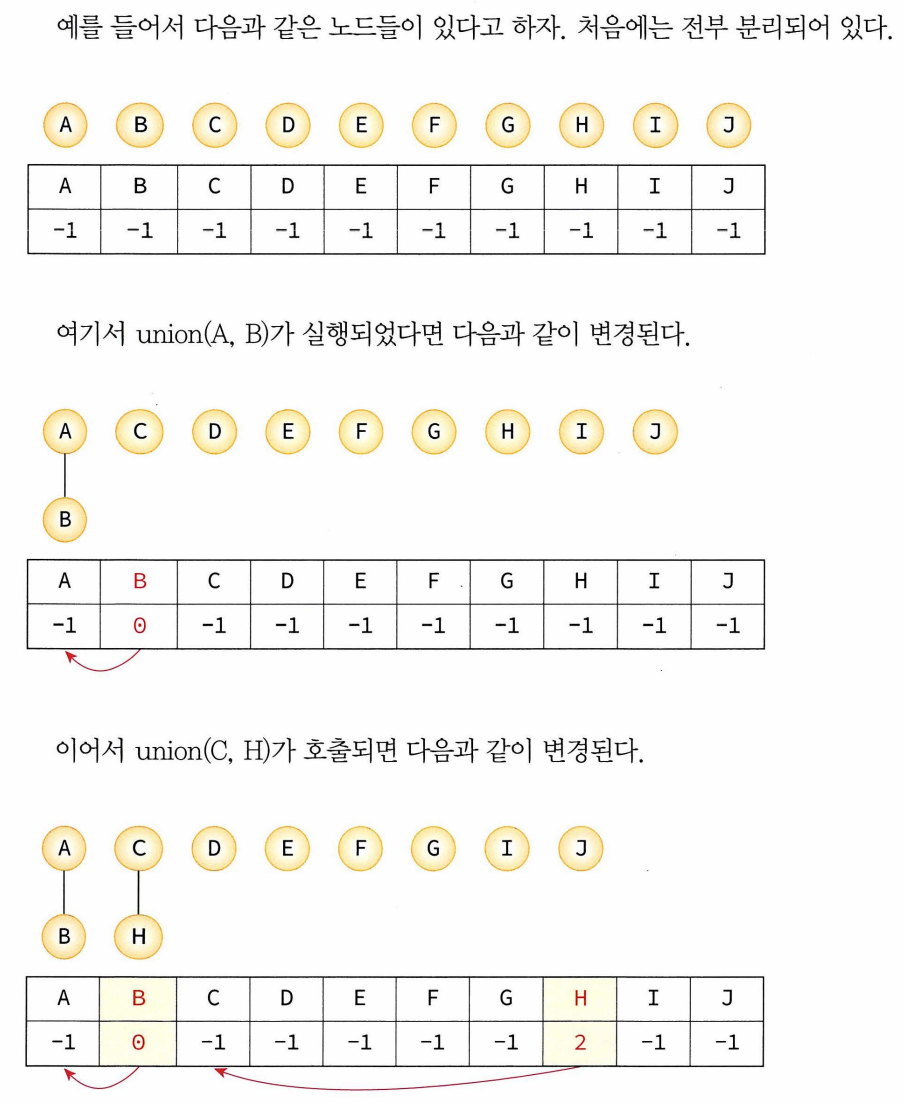
- 간선의 양 끝 정점이 같은 집합에 속해있는지 먼저 검사하는 알고리즘 : union-find 연산
- 원소 x와 y가 속해있는 집합을 입력으로 받아 2개 집합의 합집합 만듦, find(x)연산은 원소 x가 속해있는 집합 반환.
- 가장 효율적인 방법: 트리형태사용.
- 부모 포인터 표현 사용
- 각 노드에 대해 그 노드의 부모에 대한 포인터만 지칭
- 일반적인 목적(노드의 가장 왼쪽 자식, 오른쪽 자식 찾기) 작업에 부적절 but 두 노드가 같은 트리에 있나? 에 필요한 정보는 갖고 있으므로 사용 가능
- 1차원 배열로 구현 가능 : 부모노드의 인덱스 저장, 배열 값이 -1이면 부모노드 x
- 각 노드에 대해 그 노드의 부모에 대한 포인터만 지칭
- 부모 포인터 표현 사용
- 시간복잡도: union-find 알고리즘 이용하면 Kruskal의 알고리즘 시간 복잡도는 간선 정렬하는 시간에 좌우.
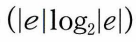
11.3 Prim의 MST 알고리즘
- Prim의 알고리즘 : 시작 정점에서부터 출발하여 신장트리집합을 단계적으로 확장해나가는 방법.
- 시작단계에서는 시작정점만이 신장트리집합에 포함
- 앞 단계에서 만들어진 신장트리집합에 인접한 정점들 중에서 최저간선으로 연결된 정점 선택하여 트리 확장. 트리가 n-1개의 간선 가질때까지 계속된다.
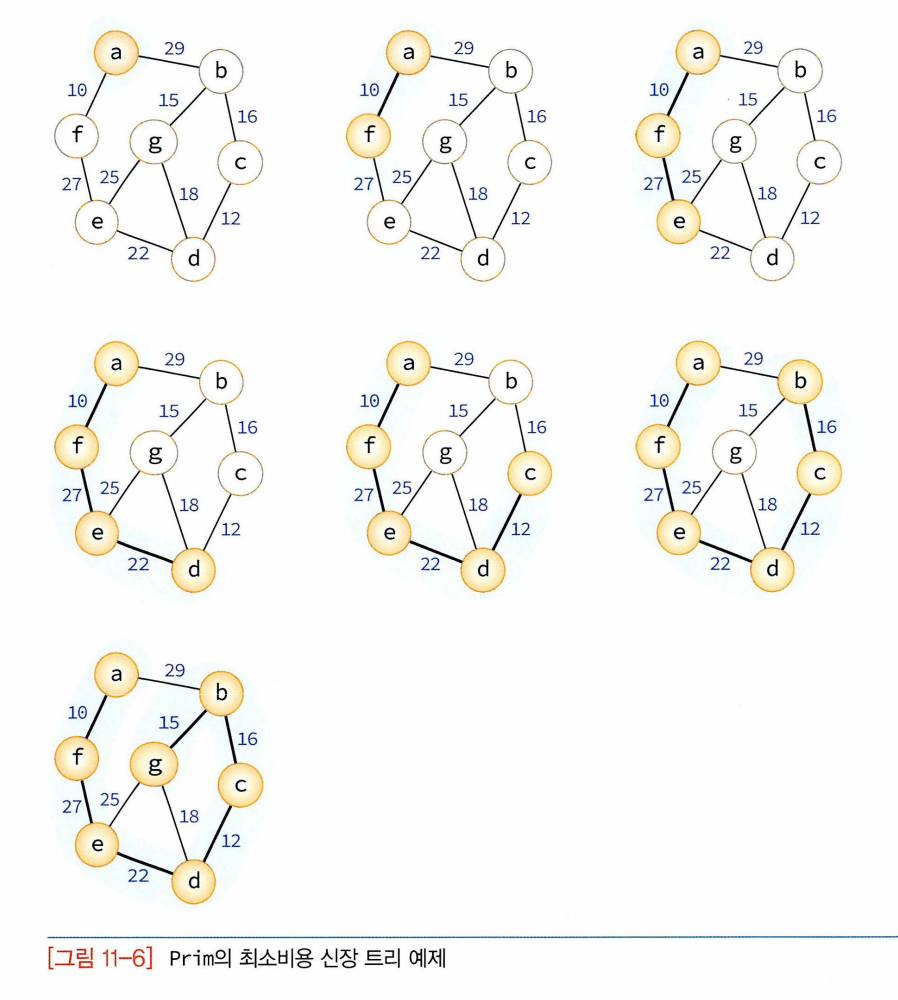
- Kruskal의 알고리즘과 비교
| Kruskal의 알고리즘 | Prim의 알고리즘 |
| 간선기반 알고리즘 | 정점기반 알고리즘 |
| 이전단계에서 만들어진 신장트리와는 상관없이 무조건 최저간선 선택 | 이전단계에서 만들어진 신장트리 확장 |
- Prim의 알고리즘은 주 반복문이 정점의 수 n만큼 반복하고, 내부 반복문이 n번 반복하므로 O(n^2)의 복잡도를 가진다.
- Kruskal의 알고리즘의 복잡도 :

>> 희소그래프(노드수보다 간선수가 적음)- Kruskal의 알고리즘, 밀집그래프(간선수보다 노드수가 적음) - Prim의 알고리즘이 유리
11.4 최단경로
- 최단경로: 네트워크에서 정점 i와 j를 연결하는 경로 중에서 간선들의 가중치 합이 최소가 되는 경로 찾기.
11.5 Dijkstra의 최단 경로 알고리즘
- 네트워크에서 하나의 시작정점으로부터 모든 다른 정점까지의 최단경로 찾는 알고리즘
- 최단 경로는 경로의 길이순으로 구해진다.
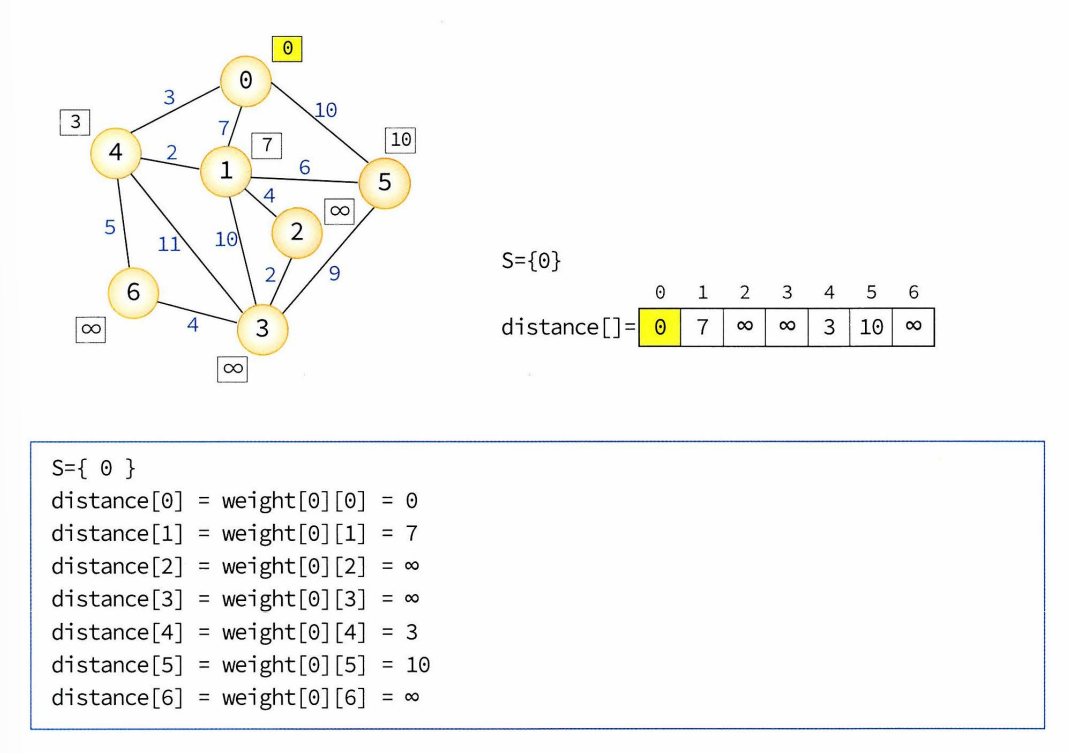
- 집합 S를 시작정점 v로부터의 최단경로가 이미 발견된 정점들의 집합이라고 할 때 시작정점에서 집합 S에 있는 정점만을 거쳐서 다른 정점으로 가는 최단거리를 기록하는 배열이 있어야 한다. 이 1차원 배열은 distance, 시작정점을 v라 하면 distance [v]=0이며 다른 정점에 대한 distance 값은 시작정점과 해당 정점간의 가중치값이 된다.
- 가중치는 보통 가중치 인접 행렬에 저장, 가중치 인접행렬을 weight라 하면 distance[w]=weight [v][w]가 된다.
- 시작단계에서는 아직 최단경로가 발견된 정점이 없음 -> S={v}일 것, 알고리즘이 진행되며 최단거리가 발견되는 정점이 S에 추가된다.
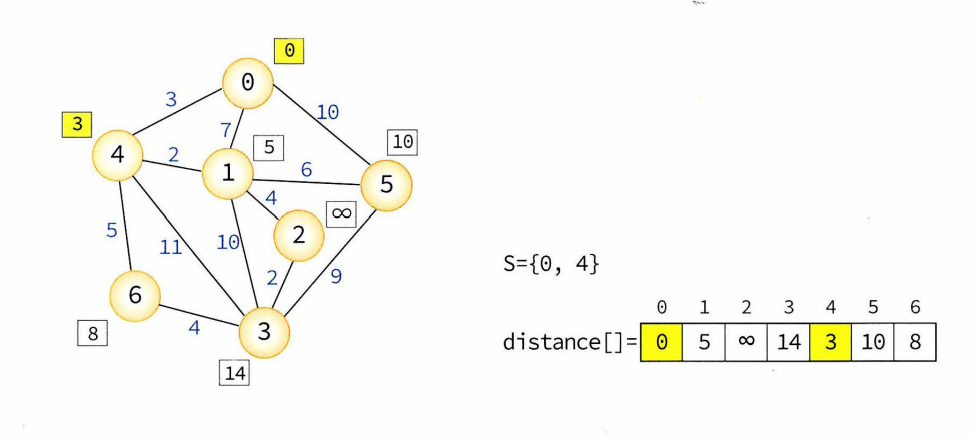
- 알고리즘의 각 단계에서 S안에 있지 않은 정점 중 가장 distance값이 작은 정점을 S에 추가.
- 현재 S에 들어있지 않은 정점 중에서 distance 값이 가장 작은 정점: u 로 설정 -> 시작정점 v에서 정점 u까지의 최단거리는 경로 1, 경로 2(2+3)은 경로 1보다 길 수밖에 없다.

- 새로운 정점 u가 S에 추가되면, S에 있지 않은 다른 정점들의 distance값 수정. 새로 추가된 정점 u를 거쳐서 정점까지 가는 거리 vs 기존거리 비교해서 더 작은 거리로 distance값 수정.

[example]



- 분석: 네트워크에 n개의 정점이 있다면 최단경로 알고리즘은 주반복문을 n번, 내부반복문을 2n번 반복 -> O(n^2)의 복잡도
11.6 Floyd의 최단 경로 알고리즘
- 모든 정점 사이의 최단경로 구하기에 Dijkstra의 알고리즘보다 더 간단하고 좋은 알고리즘(한번에 찾아줌)
2차원배열 A이용하여 3중반복하는 루프



- Dijkstra 알고리즘(두 정점 사이의 최단경로 찾기)은 시간복잡도가 O(n^2) 이므로 모든 정점쌍의 최단경로 구하려면 이 알고리즘 n번 반복해야 함> 전체 복잡도는 O(n^3). Floyd의 알고리즘은 3중반복문-> 시간복잡도: O(n^3). 그러나 매우 간결한 반복구문-> 상당히 빨리 모든 정점간 최단경로를 찾을 수 있다.
11.7 위상정렬
- 위상정렬: 방향 그래프에 존재하는 각 정점들의 선행순서를 위배하지 않으면서 모든 정점을 나열하는 것
- 알고리즘: 진입차수가 0인 정점 선택> 선택된 정점과 여기에 부착된 모든 간선 삭제> 진입차수 0인 정점의 선택과 삭제 과정 반복>모든 정점이 선택, 삭제되면 알고리즘 종료. *진입차수 0인 정점이 여러개이면 어느 정점을 선택하여도 무방.
- 이 과정에서 선택되는 정점의 수: 위상순서
- 위 과정 중 그래프에 남아있는 정점 중에 진입차수 0인 정점이 없다면 이러한 그래프로 표현된 프로젝트는 실행 불가능한 프로젝트가 되고 알고리즘이 중단된다.
- 알고리즘: 진입차수가 0인 정점 선택> 선택된 정점과 여기에 부착된 모든 간선 삭제> 진입차수 0인 정점의 선택과 삭제 과정 반복>모든 정점이 선택, 삭제되면 알고리즘 종료. *진입차수 0인 정점이 여러개이면 어느 정점을 선택하여도 무방.

- 내차수가 0인 정점 1을 시작으로 정점 1과 간선을 제거
- 다음 단계에서 정점 4의 진입차수가 0이 되므로 후보 정점은 0,4.
- 만약 정점 4 선택 -> 다음 단계에서는 오직 정점 0만이 후보
- 정점 0 선택, 정점 2가 진입차수가 0이 되어 선택가능하게 됨
- 다음에 정점 2,3,5 선택하면 140235 됨!
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] ch13. 탐색 (3) | 2024.11.25 |
|---|---|
| [자료구조] chap12. 정렬 (0) | 2024.11.19 |
| [자료구조] chap10. 그래프 I (4) | 2024.11.05 |
| [자료구조] chap9. 우선순위 큐 (0) | 2024.10.22 |
| [자료구조] chap8. 트리 (0) | 2024.10.22 |