12.1 정렬이란?
- 정렬: 물건을 크기순으로 오름차순이나 내림차순으로 나열하는 것
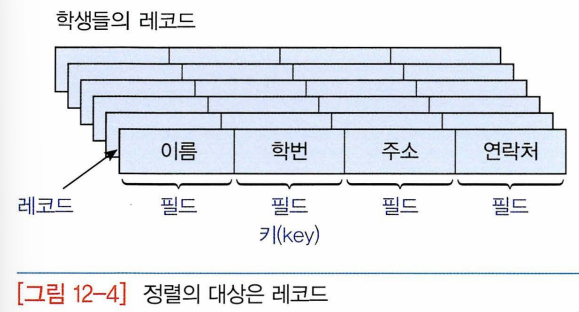
- 정렬시켜야 될 대상: 레코드, 레코드는 필드라는 단위로 나뉘어진다.
- 키: 레코드와 레코드를 식별해주는 역할을 하는 필드
- = 레코드들을 키값의 순서로 재배열
- 최적 알고리즘은 존재하지 않으므로 이들 방법 중에서 현재 환경에서 가장 효율적인 정렬 알고리즘을 선택해야 한다.
- 효율성의 기준: 정렬 위해 필요한 비교연산의 횟수와 이동연산의 횟수(빅오표기법 이용)
- 횟수는 자료의 초기화 여부에 의존적, 이동횟수와 비교횟수가 서로 비례하지 x
- 숫자와 숫자 비교는 시간 별로 안 걸림, 문자열과 문자열 비교하는 것은 상당히 시간 걸림, 숫자이동보다 큰 구조체 이동하려면 많은 시간 걸림 > 잘 맞춰서 적절한 정렬 알고리즘 선택해야 함.
- 효율성의 기준: 정렬 위해 필요한 비교연산의 횟수와 이동연산의 횟수(빅오표기법 이용)
- 정렬 알고리즘의 효율성 분류
- 단순하지만 비효율적인 방법 : 삽입정렬, 선택정렬, 버블정렬 등
- 복잡하지만 효율적인 방법 : 퀵 정렬, 히프정렬, 합병정렬, 기수정렬 등
- 자료가 적다면 단순한 정렬방법, 자료의 개수가 일정 개수 넘어가면 반드시 효율적 알고리즘 사용해야 함.
- 정렬 알고리즘의 내외부 분류
- 내부정렬 : 정렬하기 전에 모든 데이터가 메인 메모리에 올라와있는 정렬 (우리는 이것만 다룸)
- 외부정렬 : 외부 기억장치에 대부분의 데이터가 있고 일부만 메모리에 올려놓은 상태에서 정렬하는 방법
- 정렬 알고리즘의 안정성 분류
- 안정성: 입력 데이터에 동일한 키값을 갖는 레코드가 여러 개 존재할 경우 이들 레코드들의 상대적인 위치가 정렬 후에도 바뀌지 않는 것 (삽입정렬, 버블정렬, 합병정렬)
- 비안정성 : 같은 키값을 갖는 레코드들이 정렬 후에 위치가 바뀌게 될 때
12.2 선택정렬
- 선택정렬: 왼쪽 리스트와 오른쪽 리스트가 있다고 가정, 왼쪽 리스트에는 정렬이 완료된 숫자들이 들어가고 오른쪽 리스트에는 정렬되지 않은 숫자들이 들어 있음 , 초기 상태에서 왼쪽 리스트는 비어 있고 정렬되어야 할 숫자들은 모두 오른쪽 리스트에 들어 있음.--> 오른쪽 리스트에서 가장 작은 숫자를 선택하여 왼쪽 리스트로 이동하는 작업 되풀이. 오른쪽 리스트가 공백상태가 될 때까지 이 과정 되풀이.

- 제자리 정렬 : 입력배열 외에 추가적인 공간을 사용하지 않는 선택 정렬 알고리즘 (메모리 절약)
- 입력 배열에서 최소값을 발견한 다음 이 최소값을 배열의 첫번째 요소와 교환 -> 다음엔 첫번째 요소를 제외한 나머지 요소 중에서 가장 작은 값을 선택하고 이를 두 번째 요소와 교환 --> 이 절차를 (숫자 개수-1)만큼 되풀이 하면 추가적 배열 사용 없이 전체 숫자 정렬 가능
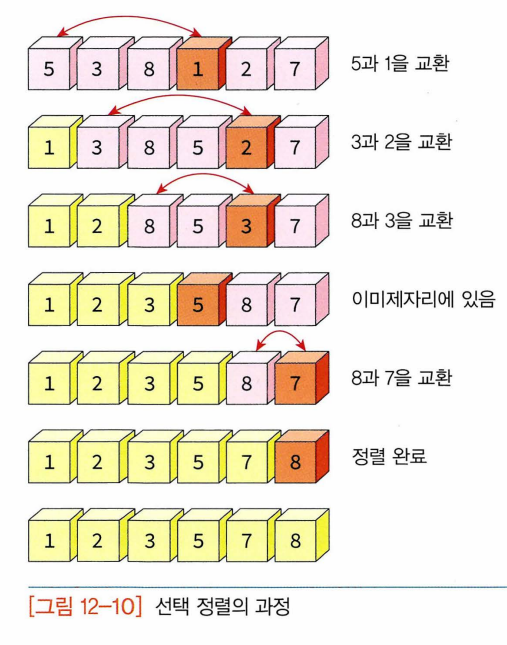
- 선택정렬의 분석
- 비교횟수 : 두 개의 for 루프 실행 횟수를 계산하면 외부루트는 n-1번, 내부루프는 0에서 n-2까지 변하는 i에 대하여 (n-1)-i번 반복된다. 키값들의 비교가 내부 루프 안에서 이루어진다.
- 전체 비교횟수 : (n-1)+(n-2)+...+1=n(n-1)/2=O(n^2)
- 레코드 교환 횟수: =외부 루트 실행횟수, 한 번 교환하기 위하여 3번의 이동이 필요함 -> 전체 이동 횟수: 3(n-1)
- 장점 : 자료 이동 횟수가 미리 결정, 이동횟수는 3(n-1)로 상당히 큼, 자료가 정렬된 경우 불필요하게 자기 자신과의 이동 ->이 문제 개선하려면 if 문 추가(최소값이 자기 자신이면 자료이동을 하지 않는다.)
- 안정성 만족 x, 값이 같은 레코드가 있는 경우 상대적인 위치가 변경될 수 O
12.3 삽입정렬
- 정렬되어 있는 리스트에 새로운 레코드를 적절한 위치에 삽입하는 과정 반복. 선택 정렬처럼 입력배열을 선택정렬과 유사하게 정렬된 부분과 정렬되지 않은 부분으로 나눠서 사용.
- 정렬되어 있지 않은 부분의 첫 번째 숫자가 정렬된 부분의 어느 위치에 삽입되어야 하는지 판단 -> 해당 위치에 이 숫자 삽입 -> 정렬된 부분의 크기는 하나 커지고 정렬이 되지 않은 부분의 크기는 하나 줄어듦. -> 삽입 연산을 정렬되지 않은 부분이 빌 때까지 반복 -> 전체 리스트가 정렬됨
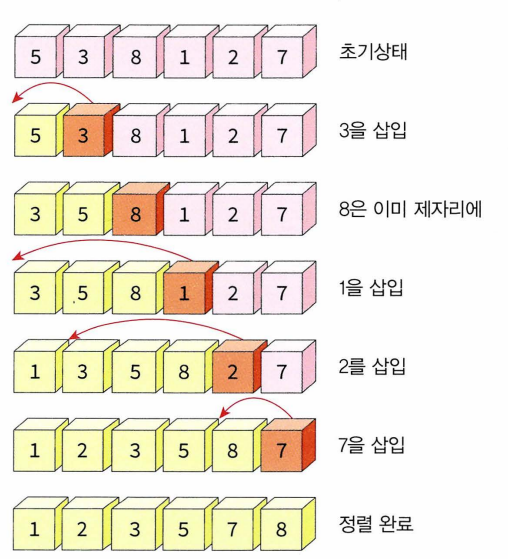
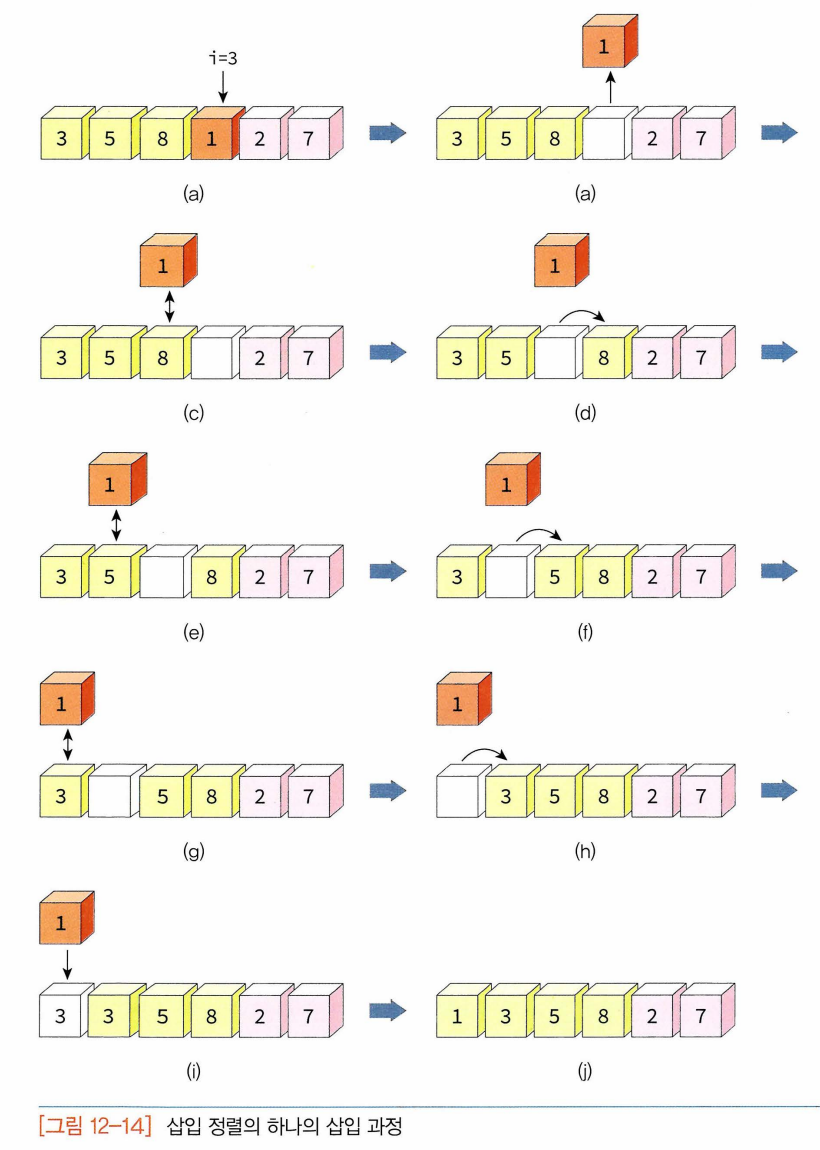
- 삽입 정렬의 복잡도 : 입력 자료의 구성에 따라 달라진다.
- 가장 빠른 경우: 입력 자료가 이미 정렬되어 있는 경우 - 삽입 정렬의 외부 루프는 n-1번 실행, 각 단계에서 1번의 비교와 2번의 이동만 이루어짐 -> 총 비교횟수는 n-1번, 총 이동횟수는 2(n-1)번 --> 알고리즘의 시간 복잡도 : O(n)
- 최악의 복잡도 : 입력 자료가 역순일 때(각 단계에서 앞에 놓인 자료들이 전부 한 칸씩 뒤로 이동해야 함)-> 외부 루프안의 각 반복마다 i번의 비교 수행
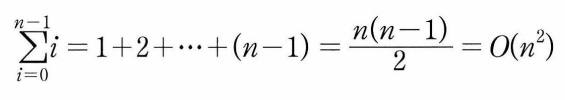
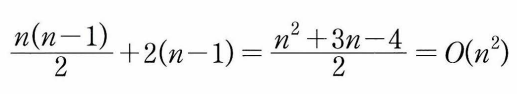
- 삽입정렬: 비교적 많은 레코드들의 이동 포함 -> 결과적으로 레코드 양이 많고 레코드 크기가 클 경우 적합하지 않음.
- 안정한 정렬방법 -> 레코드 수가 적을 경우 알고리즘 자체가 매우 간단 -> 다른 복잡한 정렬 방법보다 유리.
- 대부부분의 레코드가 이미 정렬되어 있는 경우에 매우 효율적.
12.4 버블 정렬
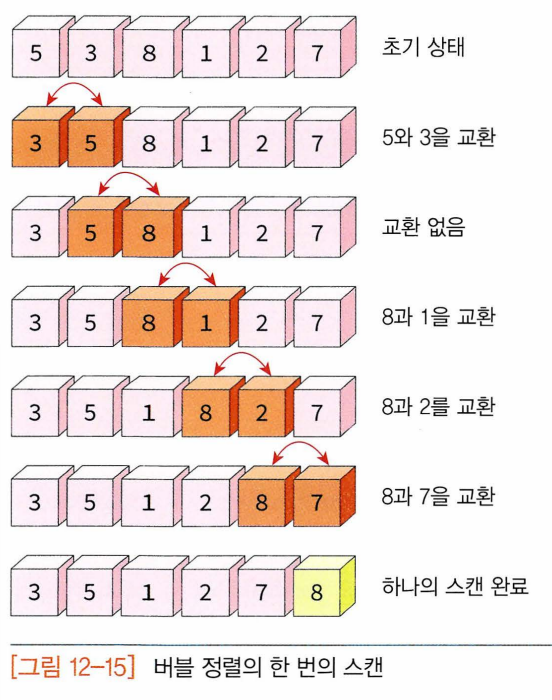
- 버블정렬: 인접한 2개의 레코드를 비교-> 크기가 순서대로 되어 있지 않으면 서로 교환하는 비교-교환 과정을 리스트의 왼쪽 끝~ 오른쪽 끝까지 진행. 이러한 리스트의 비교-교환 과정(스캔)이 한 번 완료되면 가장 큰 레코드가 리스트의 오른쪽 끝으로 이동되는 결과가 나온다. (보글보글 거품처럼 떠오름)
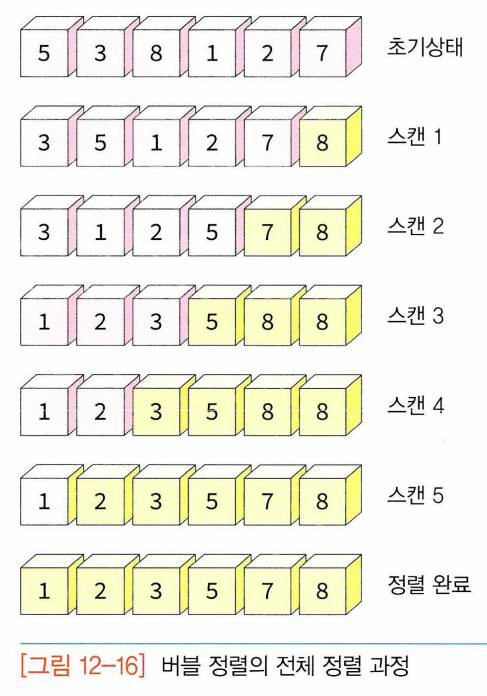
- 정렬이 안 된 오른쪽 리스트를 한 번 스캔 -> 오른쪽리스트의 오른쪽 끝에 가장 큰 레코드 위치, 오른쪽 리스트는 추가된 레코드를 포함하여 정렬한 상태 됨. 이런 스캔 과정을 정렬이 안 된 왼쪽 리스트에 반복해서 적용하면 정렬 완료.
12.5 쉘 정렬
- 쉘 정렬 : 삽입 정렬이 어느 정도 정렬된 배열에 대해서는 대단히 빠른 것 이용. 삽입정렬의 O(n^2)보다 빠르다.
- 삽입정렬의 최대 문제: 요소들이 삽입될 때 이웃한 위치로만 이동하는 것, 삽입되어야 할 위치가 현재 위치에서 멀리 떨어져 있으면 많은 이동 필요 ---> 쉘정렬이 극복(요소들이 멀리 떨어진 위치로도 이동할 수 O)
- 전체의 리스트를 한 번에 정렬하지 X, 먼저 정렬해야 할 리스트를 일정한 기준에 따라 분류 -> 연속적이지 않은 여러 개의 부분 리스트를 만듦 -> 각 부분 리스트를 삽입정렬 이용해서 정렬, 모든 부분 리스트가 정렬되면 셀정렬은 다시 전체 리스트를 더 적은 개수의 부분 리스트로 만든 후 알고리즘 되풀이. (부분 리스트 개수가 1이 될 때까지)
- 부분리스트 구성할 때는 주어진 리스트의 각 k번째 요소를 추출하여 만듦. k는 간격(gap). 셀정렬에서는 각 스텝마다 간격 k 줄여감-> 수행과정 반복될 때마다 하나의 부분 리스트에 속하는 레코드 개수는 증가. 마지막 스텝에서는 간격 값=1.
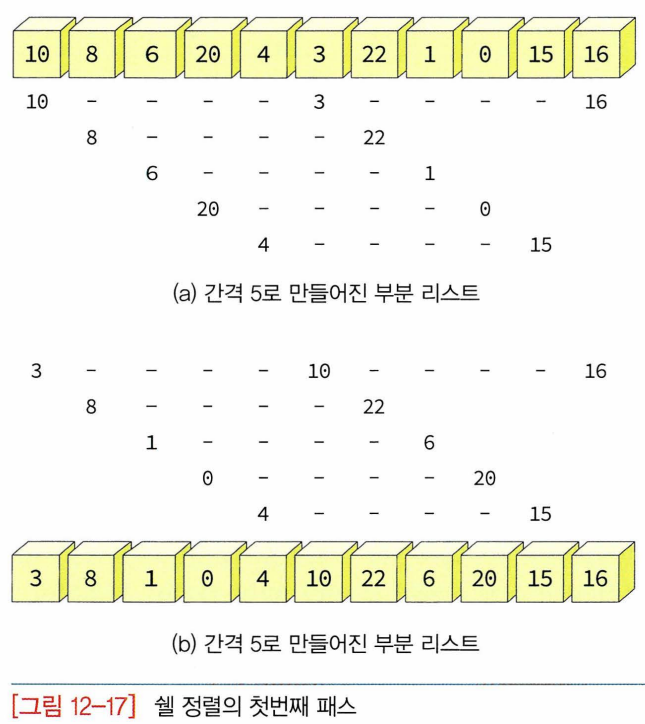
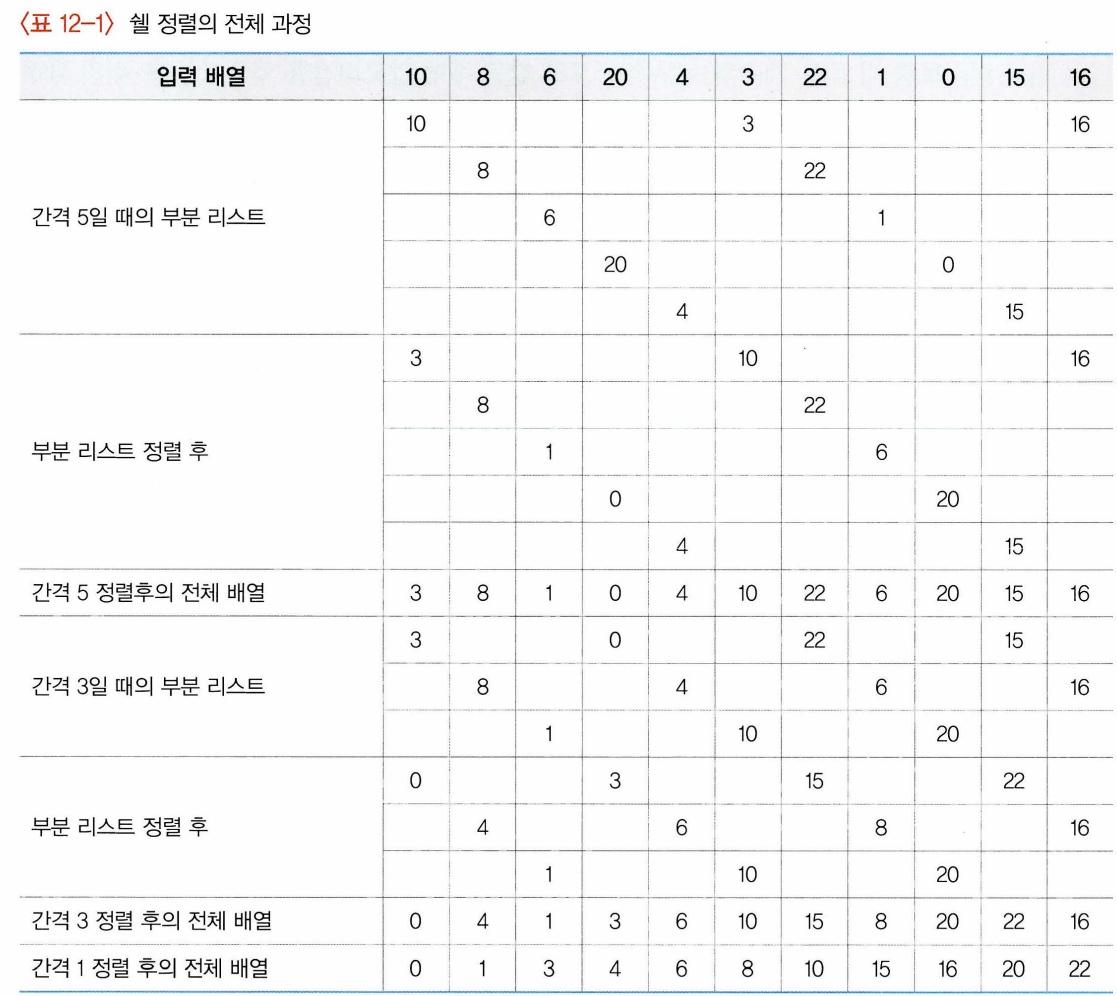
- 쉘 정렬의 분석 :
- 장점
- 연속적이지 않은 부분 리스트에서 자료의 교환 일어나면 삽입 정렬보다 더 큰 거리 이동 -> 교환되는 아이템들이 삽입정렬보다는 최종 위치에 더 가까이 있을 가능성 증가.
- 부분리스트는 어느정도 정렬이 된 상태 -> 부분리스트의 개수가 1이 되면 셀 정렬이 빠르게 수행,(삽입정렬이지만 거의 정렬된 리스트에 대해서는 빠르게 수행)
- 시간 복잡도 : 최악의 경우에는 O(n^2), 평균적인 경우 O(n^1.5)
- 장점
12.6 합병 정렬
- 합병 정렬 : 하나의 리스트를 두 개의 균등한 크기로 분할 -> 분할된 부분 리스트 정렬 -> 정렬된 부분 리스트 합해서 전체가 정렬된 리스트 얻고자 하는 것, 분할 정복 기법(문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음 결과를 모아서 원래의 문제를 해결하는 전략-분리된 문제가 아직도 해결하기 어려우면 (충분히 작지 않다면) 분할 정복방법을 연속하여 다시 적용, 주로 순환호출 이용하여 구현.) 에 바탕을 두고 있다.
- 분할 : 입력 배열을 같은 크기의 2개의 부분 배열로 분할
- 정복 : 부분 배열 정렬, 부분 배열의 크기가 충분히 작지 않으면 순환호출 이용하여 다시 분할 정복 기법 적용
- 결합 : 정렬된 부분 배열들을 하나의 배열에 통합.
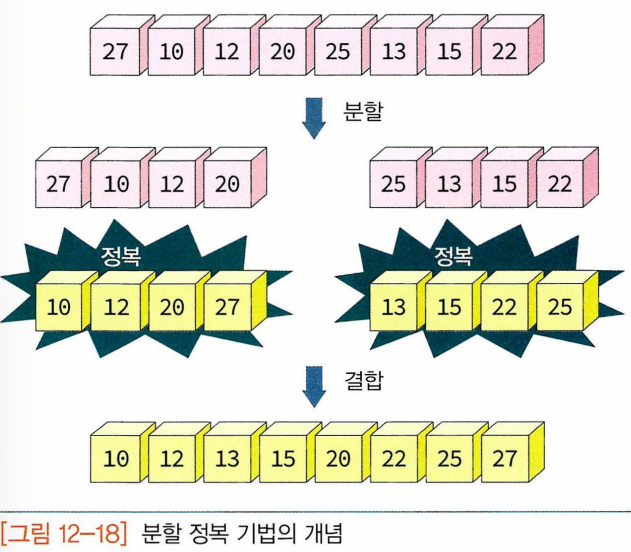
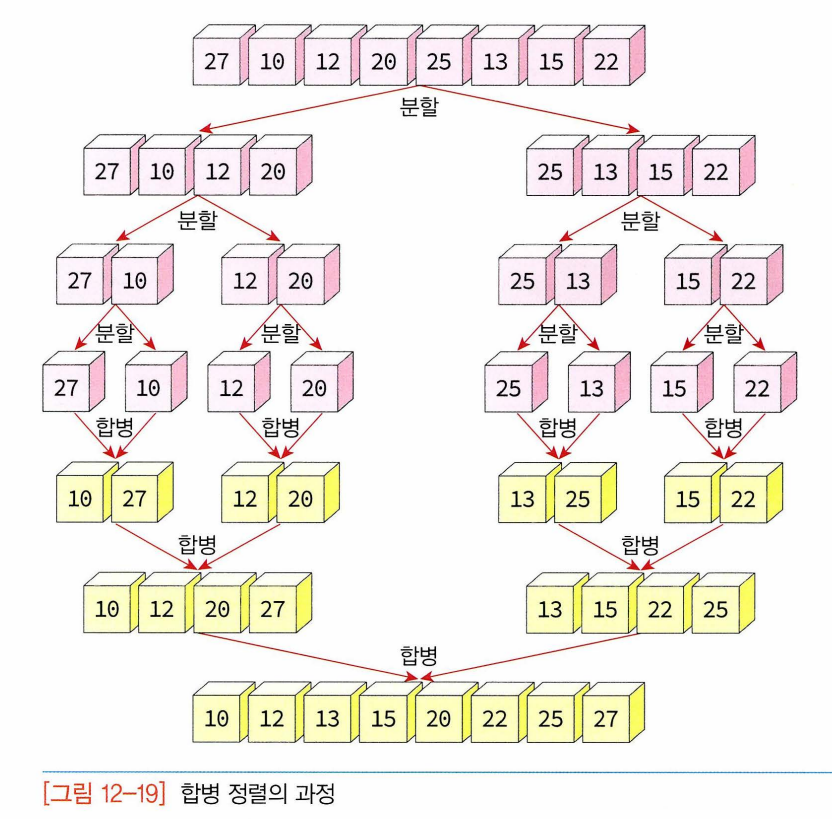
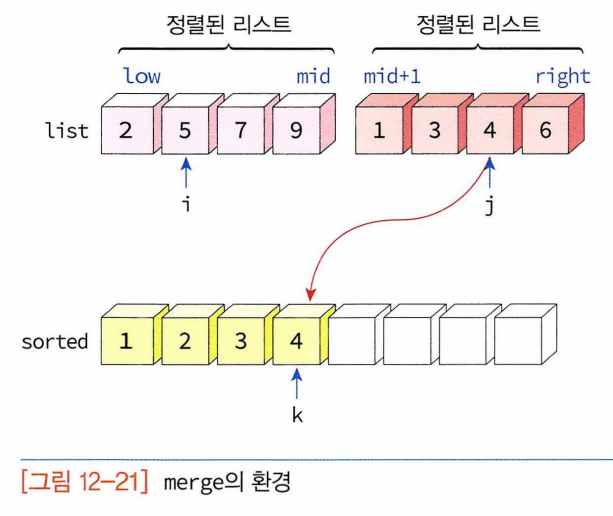
- 실제로 정렬 이루어지는 시점 : 2개의 리스트를 합병(merge) 하는 단계
- 합병정렬이 이 알고리즘 이용하게 되고 합병 자체는 어렵지 않으나 추가적인 리스트를 필요로 한다.
- 2개 리스트의 요소들을 처음부터 하나씩 비교하여 두 개의 리스트의 요소 중 더 작은 요소를 새로운 리스트로 옮긴다.(한 리스트가 먼저 끝나면 나머지 리스트의 요소들을 전부 새로운 리스트로 복사)

- 복잡도 분석
- 합병정렬은 순환호출 구조로 되어 있음 -> 레코드의 개수 n이 2의 거듭제곱이라고 가정하고 순환호출의 깊이가 얼마나 되는지 분석. n=2^3인 경우 부분 배열의 크기가 2^3-> 2^2 -> 2^1 -> 2^0으로 줄어듦 -> 순환호출의 깊이가 3임을 알 수 O. n=2^k라고 하면 부분 배열의 크기 : 2^k -> 2^k-1 -> ... -> 2^0이 되어 순환 호출의 깊이가 k가 됨.
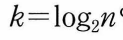
- 배열이 부분 배열로 나누어지는 단계에서는 비교연산이나 이동연산 수행 x. 부분 배열이 합쳐지는 merge 함수에서 비교연산과 이동연산 수행.(순환호출의 깊이만큼의 합병단계 필요)
- 각 합병 단계에서 수행되는 비교연산 : 일반적인 경우 하나의 합병단계에는 최대 n번의 비교연산필요.
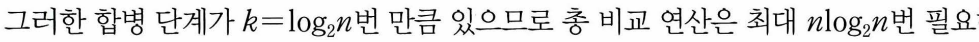
- 이동연산은? 하나의 합병 단계에서 보면 임시 배열에 복사했다가 다시 가져와야 함 -> 이동연산은 총 부분 배열에 들어있는 요소 개수가 n인경우 레코드 이동이 2n번 발생 -> 하나의 합병 단계에서 2n개

- 장점 : 안정적인 정렬 방법, 데이터 분포에 영향 덜 받음 (입력 데이터가 무엇이든 정렬되는 시간은 동일. 최악=평균=최선)
- 단점 : 임시배열 필요, 레코드들의 크기가 큰 경우 이동횟수가 많으므로 매우 큰 시간적 낭비 초래. but 레코드를 연결리스트로 구성하여 합병정렬 -> 링크 인덱스만 변경됨 -> 데이터 이동은 무시할 수 있을 정도로 작아짐 -> 크기 큰 레코드 정렬할 때 연결리스트 사용하면 합병정렬은 퀵 정렬 포함한 다른 어떤 정렬방법보다 효율적일 수 O.
12.7 퀵 정렬
- 퀵 정렬 : 평균적으로 매우 빠른 수행속도. 분할 정복법에 근거.
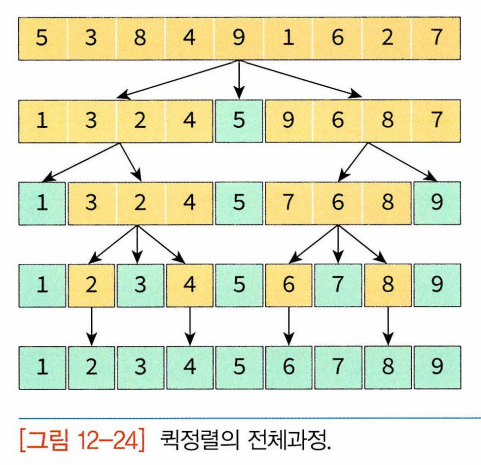
- 합병정렬처럼 전체 리스트를 2개의 부분리스트로 분할 -> 각각의 부분리스트를 다시 퀵정렬
- 합병정렬과 달리 리스트를 비균등하게 분할
- 리스트 안에 있는 한 요소-> 피벗. 피벗보다 작은 요소는 모두 피벗의 왼쪽, 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮겨짐 -> 피벗을 중심으로 왼쪽은 피벗보다 작은 요소들, 오른쪽은 피벗보다 큰 요소들로 구성 -> 피벗 제외한 왼쪽리스트, 오른쪽 리스트 다시 정렬하면 전체 리스트 형성!
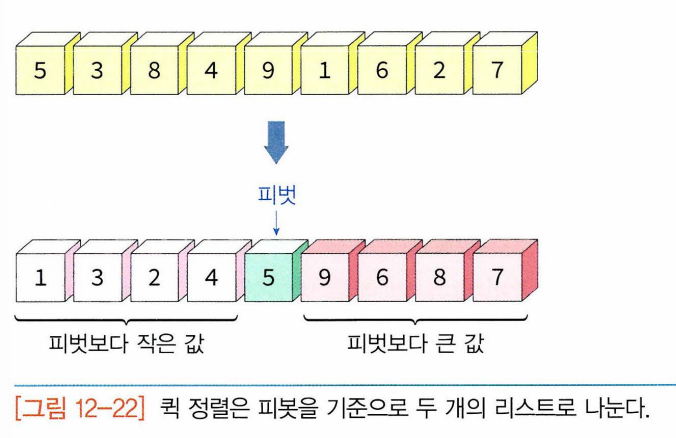
- 퀵 정렬이 피봇을 기준으로 나누어진 왼쪽 부분 리스트와 오른쪽 부분 리스트를 정렬하는 방법 : 합병 정렬과 마찬가지로 퀵 정렬 함수가 다시 부분리스트에 대하여 순환호출 -> 부분리스트에서도 다시 피봇을 정하고 피봇을 기준으로 2개의 부분 리스트로 나누는 과정 되풀이(부분 리스트들이 더 이상 분할이 불가능할때까지)
- 가장 중요한 함수 : partition 함수(데이터가 들어있는 배열 list의 left부터 right까지의 리스트를 피봇을 기준으로 2개의 부분리스트로 나누게 된다. -피벗보다 작은 데이터 : 모두 왼쪽 부분 리스트, 큰 데이터 : 모두 오른쪽 부분 리스트
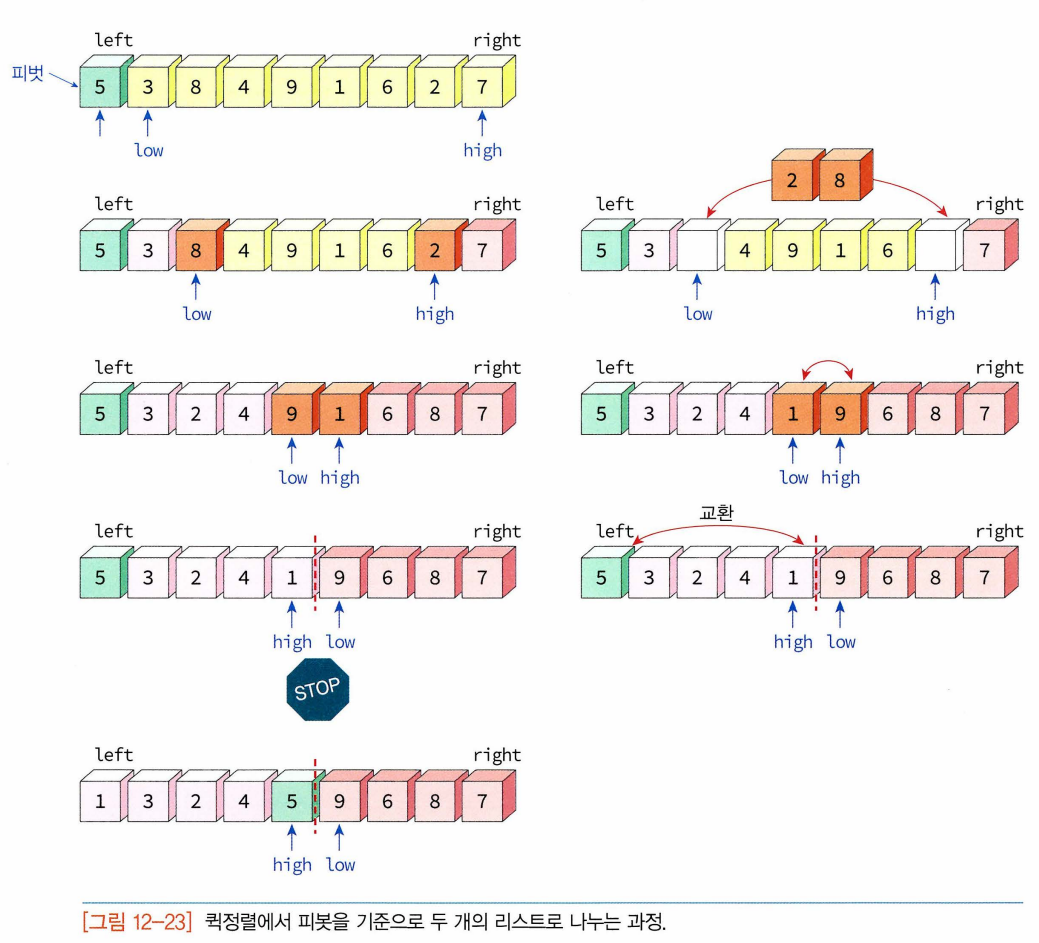
- 이 과정이 끝난 후 피벗을 제외한 왼쪽리스트(1,3,2,4)를 독립적으로 다시 퀵정렬하고 오른쪽 리스트 (9,6,8,7)을 다시 퀵정렬
- 복잡도 분석
- n이 2의 거듭제곱이라고 가정, 만약 퀵정렬에서의 리스트 분할이 항상 리스트의 가운데에서 이루어짐 -> 합병 정렬의 복잡도 분석처럼 n개의 레코드를 갖는 리스트는 n/2^k의 크기로 나누어짐(크기가 1이 될 때까지)

최선의 경우 : 합병정렬처럼 균등하게 나뉠 때
최악의 경우 : 리스트가 계속 불균형하게 나뉠 때 :레코드의 수만큼 총 n번의 패스 실행, 각 패스에서 n번의 비교 -> 비교연산을 n^2번 실행. ---> (O(n^2)
- 장점 : 속도 빠르고 추가메모리공간을 필요로 하지 않음 / 단점 : 정렬된 리스트에 대해서는 오히려 수행시간 더 많이 걸림 --> 이러한 불균형분할 방지를 위해 피벗을 선택할 때 리스트의 왼쪽데이터보다는 리스트의 중앙부분을 분할할 수 있는 데이터 선택. 리스트 내의 중간값 피벗으로 선택. 리스트의 왼쪽, 오른쪽, 중간 3개의 데이터 중 중간 값을 선택하는 방법이 많이 사용
12.8 히프 정렬
- 히프 : 우선순위 큐를 완전 이진 트리로 구현하는 방법. 최댓값이나 최솟값을 쉽게 추출할 수 있는 자료구조. 히프에는 최소히프와 최대히프가 있고 정렬에서는 최소 히프를 사용하는 것이 프로그램을 쉬워지게 한다.
- 최소 히프: 부모 노드의 값이 자식 노드의 값보다 작음 -> 최소히프의 루트노드 : 가장 작은 값을 갖게 된다.
- 정렬할 배열을 먼저 최소히프로 변환, 가장 작은 원소부터 차례대로 추출하여 정렬
- 히프는 1차원 배열로 쉽게 구현될 수 O. 최소히프를 만들고 숫자들을 차례로 삽입한 후 최솟값부터 삭제.
- 최소 히프: 부모 노드의 값이 자식 노드의 값보다 작음 -> 최소히프의 루트노드 : 가장 작은 값을 갖게 된다.
12.9 기수 정렬
- 기수정렬(radix sort) : 레코드를 비교하지 않고도 정렬하는 방법. 입력 데이터에 대해 어떤 비교 연산도 실행하지 않고 데이터를 정렬할 수 있는 색다른 정렬 기법. 다단계 정렬, 단계의 수는 데이터의 자리수의 개수와 일치.
* 기수 : 숫자의 자리수
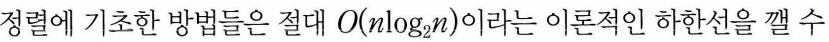
- 기수정렬은 O(kn)의 시간 복잡도를 가지는데 대부분 k<4이하.
- 문제는 기수정렬이 추가적인 메모리를 필요로 한다. 이를 감안해도 기수정렬이 다른 정렬 기법보다 빠르기 때문에 데이터를 정렬하는 상당히 인기 있는 정렬기법 중 하나.
- 단점 : 정렬할 수 있는 레코드의 타입 한정(레코드의 키들이 동일한 길이를 가지는 숫자나 문자열로 구성돼있어야 함, 숫자로 표현되지 않으면 매우 많은 버킷이 필요하게 되므로 기수정렬 적용이 불가능.) but 다른 정렬방법들은 모든 키 형태에 적용될 수 o
- 문제는 기수정렬이 추가적인 메모리를 필요로 한다. 이를 감안해도 기수정렬이 다른 정렬 기법보다 빠르기 때문에 데이터를 정렬하는 상당히 인기 있는 정렬기법 중 하나.
- 동작원리
- 한자리수의 숫자 정렬 : 각 자리수의 값에 따라 버킷에 넣고 빼는 동작 되풀이
2. 여러자리로 이루어진 수 : 1의 자리수와 10의 자리수를 따로 사용하여 정렬 - 먼저 낮은 자리수로 정렬한 다음 차츰 높은 자리수로 정렬해야 한다.
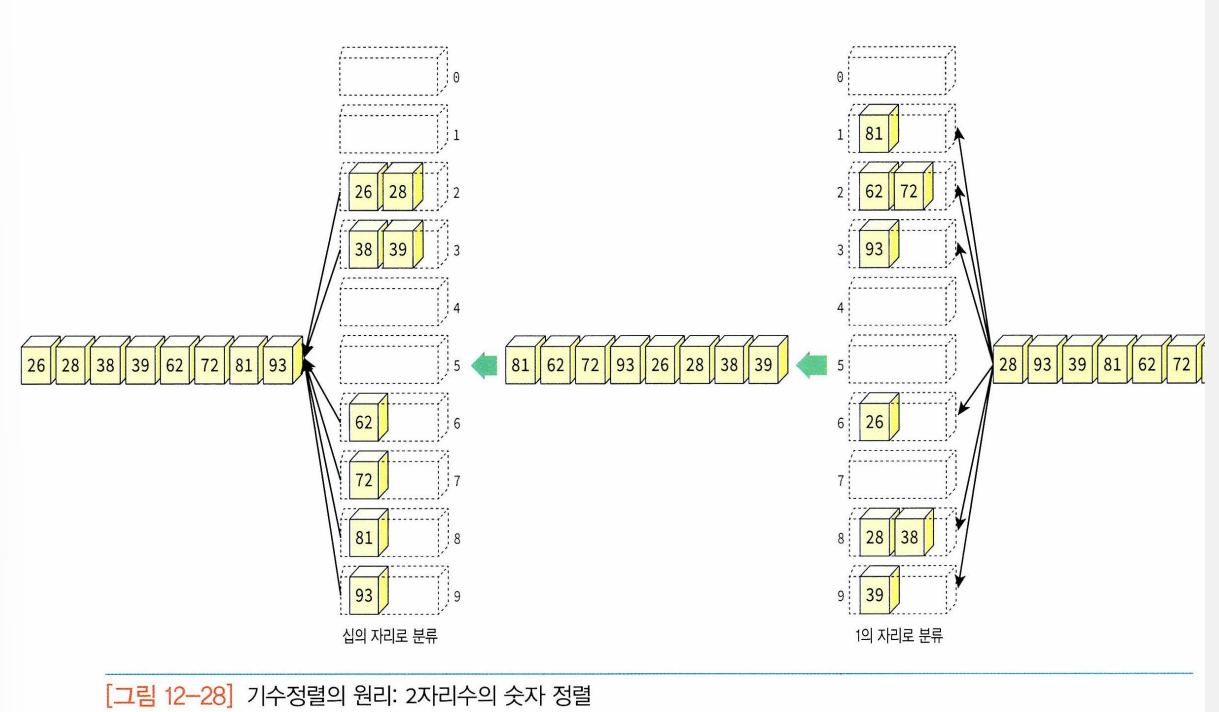
- 각각의 버킷에서 먼저 들어간 숫자들은 먼저 나와야 한다. 따라서 각각 버킷은 큐로 구현되어야 한다. (그래야 리스트 상에 있는 요소들의 상대적인 순서 유지) - 버킷에 숫자를 집어넣는 연산은 큐의 삽입연산, 숫자를 읽는 연산은 삭제연산으로 대치
- 키의 표현방법과 밀접한 관계. 키를 2진법을 사용하여 정렬 -> only 2개 필요, 키가 알파벳 문자로 돼있으면 26개 필요
- 입력리스트가 n개의 정수 갖고 있다 하면 알고리즘 내부 루프는 n번 반복. 각 정수가 d개의 자리수 갖고 있다 하면 외부루프는 d번 반복 --> O(d*n)의 시간복잡도 가짐. but 일반적으로 정수크기의 제한에 의해 d는 n에 비해 아주 작은 수 -> O(n)이라 해도 됨.
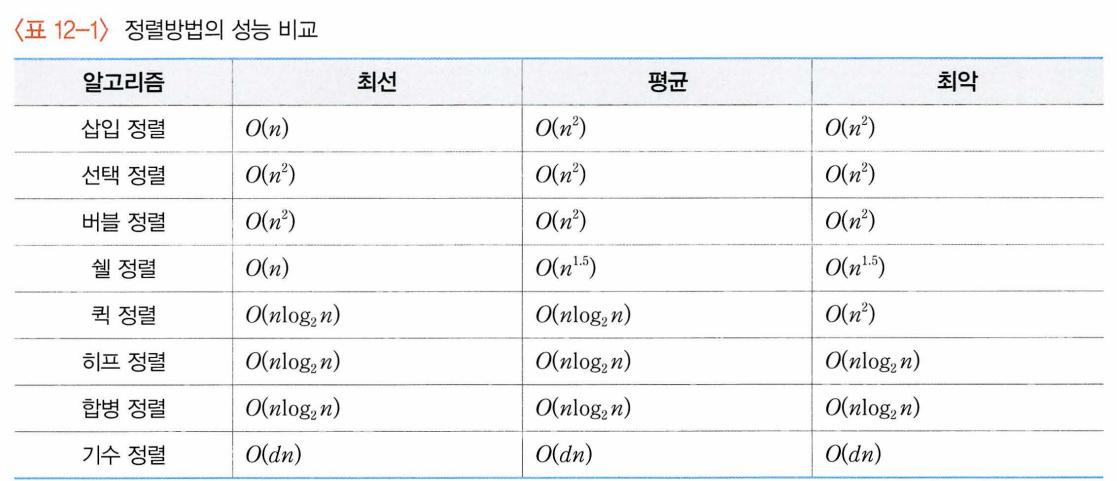
12.10 정렬 알고리즘의 비교

'CS > 자료구조' 카테고리의 다른 글
| [자료구조] ch14. 해싱 (2) | 2024.11.29 |
|---|---|
| [자료구조] ch13. 탐색 (3) | 2024.11.25 |
| [자료구조] chap11. 그래프 II (1) | 2024.11.12 |
| [자료구조] chap10. 그래프 I (4) | 2024.11.05 |
| [자료구조] chap9. 우선순위 큐 (0) | 2024.10.22 |