14.1 해싱이란?
- 선형탐색이나 이진탐색은 모두 키를 저장된 키값과 반복적으로 비교함으로써 탐색하고자 하는 항목에 접근-> 최대 가능한 시간 복잡도가 O(로그n)에 그친다. 어떤 응용에서는 더 빠른 탐색 알고리즘 요구
- 해싱은 O(1)의 시간 안에 탐색 끝마칠수도 있다.
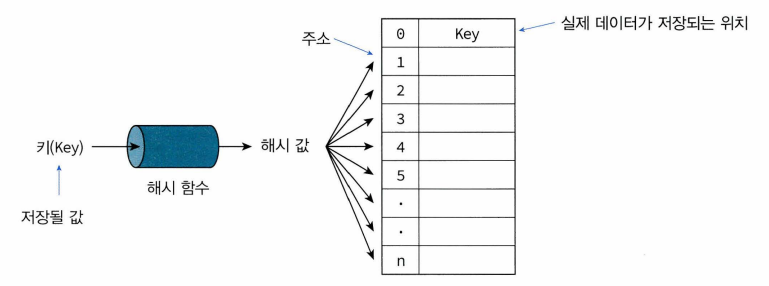
- 키에 산술적인 연산 적용 -> 항목이 저장돼있는 테이블의 주소를 계산한여 항목에 접근.
- 해시테이블: 키에 대한 연산에 의해 직접 접근 가능한 구조
- 해싱: 해시테이블 이용한 탐색
14.2 추상자료형 사전
- 사전 : (키,값)쌍의 집합. 키와 관련된 값을 동시에 저장하는 자료구조. (키,값)쌍을 저장할 수도 있고 삭제할수도 있으며 키를 가지고 값을 검색할 수 있다. map이나 table로 불리기도 한다.
- 키 : 사전의 단어처럼 항목과 항목을 구별시켜주는 것
- 값 : 단어의 설명
- 항목들이 모두 키를 가지고 있다는 점, 오직 키에 의해서만 관리된다는 점에서 다른 자료구조(ex. 리스트-근본적으로 위치에 의해 관리됨)와는 구분됨.
- 사전의 연산

이진탐색트리를 가지고도 추상자료형 사전 구현 가능, 만약 이진탐색트리를 사용한다면 최악의 경우 시간복잡도는 O(n), 사전구조를 가장 효율적으로 구현할 수 있는 방법 -> 해싱!! : 키의 비교가 아닌 키에 수식을 적용시켜서 바로 키가 저장된 위치를 얻는 방법.
14.3 해싱의 구조
- 현실적으로 탐색키들이 문자열이거나 매우 큰 숫자이기 때문에 탐색키를 직접 배열의 인덱스로 사용하기에 무리있음 -> 각 탐색키를 작은 정수로 mapping시키는 함수 필요.
- 해싱에서는 자료 저장하는데 배열 사용.
- 원하는 항목이 들어있는 위치를 알고 있다면 매우 빠르게 자료를 삽입하거나 꺼낼 수 o. 배열의 다른 요소에는 전혀 접근할 필요 x.
- 해싱은 이렇게 어떤 항목의 키만을 가지고 바로 항목이 들어있는 배열의 인덱스를 결정하는 기법.
- 해시함수: 키를 입력으로 받아 해시 주소를 생성하고, 해시주소를 해시 테이블의 인덱스로 활용한다.
- 이 배열의 인덱스위치에 자료 저장 가능, 저장된 자료를 꺼낼수도 있음

- 해시테이블 ht는 M개의 버킷으로 이루어지는 테이블, ht[0], ht[1],...,ht[M-1]의 원소 가짐.
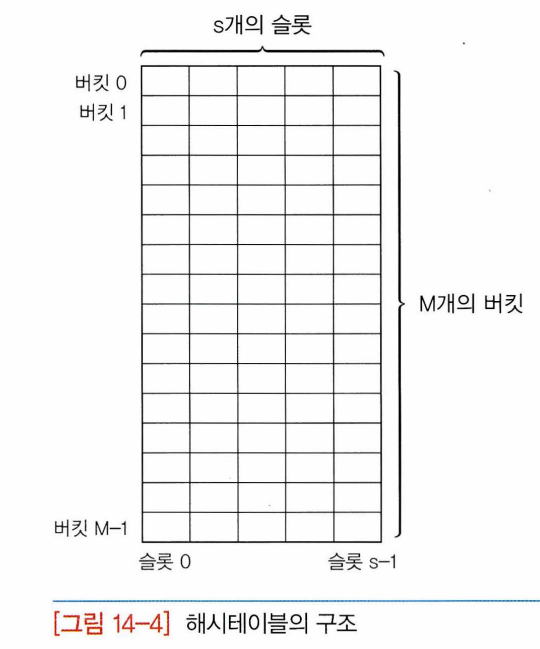
- 하나의 버킷은 s개의 슬롯을 가질 수 있으며 하나의 슬롯에는 하나의 항목 저장
- 하나의 버킷에 여러 개의 슬롯을 두는 이유 : 서로 다른 두 개의 키가 해시함수에 의해 동일한 해시 주소로 변환될 수 있음 -> 여러 개의 항목을 동일한 버킷에 저장
- 그러나 대부분의 경우 하나의 버킷은 하나의 슬롯 가짐
- 해시 테이블에 존재하는 버킷의 수 : M, 해시함수 h는 모든 키에 대해 0<=h(x)<=M-1의 범위의 값 제공해야 함.
- 대부분의 경우 해시 테이블 버킷 수는 모든 키의 경우의 수보다 매우 작음 -> 여러 개의 서로 다른 키가 해시함수에 의해 같은 해시주소로 사상(mapping)되는 경우가 자주 발생
- 충돌 : 서로 다른 두 개의 키 k1과 k2에 대해 h(k1)=h(k2)인 경우, 키 k1, k2는 동의어.
- 충돌 발생하면 같은 버킷에 있는 다른 슬롯에 항목 저장. 충돌 자주발생 -> 버킷내부에서의 순차탐색시간 길어져 탐색성능 저하 가능 -> 해시함수 수정하거나 해시테이블 크기 적절히 조절해야함.
- 충돌이 버킷에 할당된 슬롯 수보다 많이 발생 -> 버킷에 더 이상 항목 저장할 수 없게 되는 오버플로우 발생.(버킷 당 슬롯의 수가 하나(s=1)-> 충돌이 곧 오버플로우. -> 더이상 항목 저장할 수 없게 되므로 해결해야함!
- 충돌 : 서로 다른 두 개의 키 k1과 k2에 대해 h(k1)=h(k2)인 경우, 키 k1, k2는 동의어.
- 대부분의 경우 해시 테이블 버킷 수는 모든 키의 경우의 수보다 매우 작음 -> 여러 개의 서로 다른 키가 해시함수에 의해 같은 해시주소로 사상(mapping)되는 경우가 자주 발생
- 이상적인 해싱의 예시: 학생들의 인적사항 해싱으로 저장 -> 해싱테이블에는 학생들의 인적사항 저장돼있고 학번을 키로 설정.(다른부분만)
- 해시테이블에 자료 저장하는데 필요한 시간 : O(1) - 해시함수 계산하는 시간만 필요
- 자료 꺼낼때도 학번을 갖고 해시함수를 계산하여 나온 위치에 있는 자료 꺼내면 됨.
- 자료 꺼내고 넣을 때 전체 배열 탐색 X.

- 실제의 해싱: 실제로 해시테이블 제한 -> 하나의 키당 해시테이블에서 하나의 공간 할당할 수 X
- 보통의 경우 키 매우 많고 해시테이블의 크기는 상당한 제약 받음. -> 일반적인 경우는 키에 비해 해시테이블의 크기 작음, 일반적으로 키 중 일부만 사용 -> 전체 위한 공간을 항상 준비할 필요 X -> 더 작은 해시테이블 사용하는 해시함수 고안
- 간단하며 강력한 방법 : 키를 해시테이블의 크기로 나눠서 그 나머지를 해시 테이블의 주소로 하는 것
- 정수 i를 해시테이블크기 M으로 나눠서 나머지 취해보면 0에서 M-1까지의 숫자가 생성 -> 해시테이블을 위한 유효한 인덱스가 됨, 나머지 구하는 연산자인 mod사용하면 해시함수는 다음과 같이 표시 --> h(k)=k mod M
- 완벽한 해시함수 x-> 두개이상의 키가 동일한 해시테이블의 공간으로 사상될 수 o ->충돌발생
- 저장되는 과정에서 계속 충돌과 오버플로우가 일어나는 예시
- 정수 i를 해시테이블크기 M으로 나눠서 나머지 취해보면 0에서 M-1까지의 숫자가 생성 -> 해시테이블을 위한 유효한 인덱스가 됨, 나머지 구하는 연산자인 mod사용하면 해시함수는 다음과 같이 표시 --> h(k)=k mod M

- 실제 해싱에서는 충돌과 오버플로우 빈번하게 발생 -> 시간복잡도는 이상적인 O(1)보다는 떨어지게 됨
14.4 해시함수
- 키값을 해시테이블의 주소로 변환, 잘 설계돼야 탐색효율 증가
- 좋은 해시함수의 조건
- 충돌이 적어야 함
- 해시함수 값이 해시테이블 주소영역 내에서 고르게 분포
- 계산 빨라야 함
- 해시테이블의 크기가 M인 경우 해시함수는 키(주로 정수거나 문자열)들을 [0, M-1]의 범위의 정수로 변환시켜야 함
{키들이 정수일 경우}
- 제산함수 : 나머지 연산자(mod)를 사용하여 키를 해시 테이블의 크기로 나눈 나머지를 해시 주소로 사용하는 방법, 키 k에 대해 해시함수는 h(k)=k mod M
-
- M: 해시테이블의 크기, 해시함수 값의 범위는 0~(M-1). 해시 테이블의 인덱스로 사용하기에 이상적인 값. 가장 일반적인 해시 함수로서 테이블의 크기 M은 주로 소수 선택 - 다양한 응용분야에 쉽게 적용할 수 있음+해시주소를 상당히 고르게 분포시키는 좋은 방법
- M의 선택이 중요한 이유 : 메모리주소를 갖고 해싱을 한다면 M이 짝수라면 k mod M은 k가 짝수이면 짝수가 되고 홀수라면 홀수가 됨, 메모리 주소는 보통 2의배수 -> k가 짝수가 될 가능성 높음-> 해시주소가 한쪽으로 편향되게 됨-> 해시테이블 골고루 사용하지 않는 것.
- 따라서 테이블 크기 M은 항상 홀수여야 함. M이 소수라면 k mod M은 0에서 M-1을 골고루 사용하는 값 만들어냄
- 나머지 연산을 수행했을 때 음수가 나올 가능성에 대비 -> k mod M이 음수라면 여기에 M을 더해 결과값이 항상 0에서 M-1이 되도록 해야 함
- M: 해시테이블의 크기, 해시함수 값의 범위는 0~(M-1). 해시 테이블의 인덱스로 사용하기에 이상적인 값. 가장 일반적인 해시 함수로서 테이블의 크기 M은 주로 소수 선택 - 다양한 응용분야에 쉽게 적용할 수 있음+해시주소를 상당히 고르게 분포시키는 좋은 방법
-

- 폴딩함수 : 주로 키가 해시 테이블의 크기보다 더 큰 정수인 경우 사용
- 키의 일부만 사용하는 것이 아니고 키를 몇 개의 부분으로 나누어 이를 더하거나 비트별로 XOR같은 부울연산을 하는 것이 보다 좋은 방법.
- ex. 키는 32비트이고 해시테이블의 인덱스는 16비트 정수인 경우
- 키의 앞의 16비트를 무시하고 뒤의 16비트를 해시코드로 사용한다면 앞의 16비트만 다르고 뒤의 16비트는 같은 키의 경우 충돌이 발생할 것이다. -> 32비트 키를 2개의 16비트로 나누어 비트별로 XOR연산을 함 -> hash_index = (short) (key ^ (key>>16))
- 키를 여러 부분으로 나누어 모두 더한 값을 해시주소로 사용.
- 키를 나누고 더하는 방법:
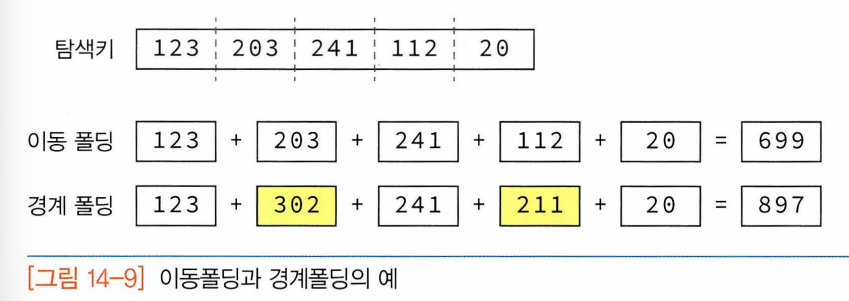
- 이동폴딩: 키를 여러 부분으로 나눈 값들을 더하여 해시 주소로 사용
- 경계폴딩: 키의 이웃한 부분을 거꾸로 더하여 해시주소 얻음
- 폴딩 방법 구현 : 키 값을 해시 테이블 크기만큼의 수를 가지는 부분으로 분할, 분할된 부분을 합하여 해시함수를 만들어줌.
- 키를 나누고 더하는 방법:
- ex. 키는 32비트이고 해시테이블의 인덱스는 16비트 정수인 경우
- 키의 일부만 사용하는 것이 아니고 키를 몇 개의 부분으로 나누어 이를 더하거나 비트별로 XOR같은 부울연산을 하는 것이 보다 좋은 방법.
- 중간 제곱 함수: 키를 제곱한 다음 중간의 몇 비트를 취해서 해시주소 생성. 제곱값의 중간 비트들은 대개 키의 모든 문자들과 관련있음 -> 서로 다른 키는 몇 개의 문자가 같을지라도 서로 다른 해싱주소 갖게됨. 키 값 제곱한 값의 중간 비트들의 값은 비교적 고르게 분산
- 비트 추출 방법: 해시 테이블의 크기가 M=2^k일 때 키를 이진수로 간주, 임의의 위치의 k개의 비트를 해시주소로 사용.
- 매우 간단 but 키의 일부 정보만을 사용하므로 해시 주소의 집중현상이 일어날 가능성 높음
- 숫자 분석 방법 : 숫자로 구성된 키에서 각각의 위치에 있는 수의 특징을 미리 알고 있을 때 유용.
- 키의 각각의 위치에 있는 숫자 중 편중되지 않는 수들을 해시 테이블의 크기에 적합한 만큼 조합-> 해시 주소로 사용
- ex. 학번이 200212345일 때 입학년도 의미하는 앞 4자릿수 편중-> 가급적 사용하지 않고 나머지 수 조합하여 해시주소로 활용
- 키의 각각의 위치에 있는 숫자 중 편중되지 않는 수들을 해시 테이블의 크기에 적합한 만큼 조합-> 해시 주소로 사용
{탐색키가 문자열일 경우}
- 많은 경우 키들이 문자열, 문자열로부터 좋은 해시주소를 생성하는 것이 중요. 대개 문자열 안의 문자에 정수를 할당하여 바꿈, 가장 보편적인 방법은 문자의 아스키 코드값이나 유니코드값을 사용하는 것.
- 첫번째 문자의 아스키 코드값을 해시 주소로 사용하는 것- > 구별불가능할 수 있음.
- 문자열 안의 모든 문자를 골고루 사용
- 각 문자의 아스키 코드값 다 더하기(가장 보편적) : 서로 다른 키들이 같은 문자로 이루어져 있지 않는 한 잘 동작
- 문제점: 위치가 다른경우 구별 불가 ex. cup, puc / 아스키 문자코드의 범위가 65~112이기에 만약 3자리로 이루어진 키의 경우 195~366으로 해시코드 집중.
- 글자들의 아스키코드값에 위치에 기초한 값 곱하기(더 좋은 방법) : 글자들의 아스키 코드 값에 위치에 기초한 값 곱함 -> 문자열 s가 n개의 문자 갖고 있다고 가정, s안의 i번째 문자가 ui라 하면 해시 주소는 다음과 같이 계산
- 각 문자의 아스키 코드값 다 더하기(가장 보편적) : 서로 다른 키들이 같은 문자로 이루어져 있지 않는 한 잘 동작
- 문자열 안의 모든 문자를 골고루 사용

- 키가 긴 문자열로 되어 있을 경우 오버플로우를 일으킬 수 o.C언어에서는 오버플로우 무시 -> 여전히 유효한 해시주소 얻을 수 O. 보통 g의 값으로는 31 사용, 오버플로우 발생하면 해시코드 값이 음수가 될 수 o. (이런 경우를 검사해야함)
14.5 개방 주소법
- 충돌: 서로 다른 키를 갖는 항목들이 같은 해시주소 갖는 현상
- 충돌이 발생하고 해시주소에 더 이상 빈 버킷이 남아있지 않으면 오버플로우 발생, 오버플로우 발생하면 해시테이블에 항목을 더 이상 저장하는 것 불가능 -> 해결해야 함
- 해결방법:
- 개방주소법: 충돌이 일어난 항목을 해시 테이블의 다른 위치에 저장, 특정 버키셍서 충돌이 발생하면 비어있는 버킷 찾음. 비어잇는 버킷에 항목 저장.
- 해시테이블에서 비어있는 공간 찾는 것 : 조사(probing), 여러 가지 방법의 조사 가능
- 선형조사법, 이차조사법, 이중해싱법, 임의조사법
- 체이닝: 해시테이블의 하나의 위치가 여러개의 항목을 저장할 수 있도록 해시테이블의 주소 변경
- 개방주소법: 충돌이 일어난 항목을 해시 테이블의 다른 위치에 저장, 특정 버키셍서 충돌이 발생하면 비어있는 버킷 찾음. 비어잇는 버킷에 항목 저장.
선형조사법
- 충돌이 ht[k]에서 발생했다면 ht[k+1]이 비어있는지 살펴봄. 비어있지 않다면 ht[k+2]를 살펴봄 -> 비어있는 공간 나올때까지 계속해서 조사.
- 테이블의 끝에 도달하게 되면 다시 테이블의 처음으로 감. 조사를 시작했던 곳으로 되돌아오게 되면 테이블이 가득 찬 것으로 판단.
- 조사되는 위치 : h(k), h(k) + 1, h(k) +2, h(k) +3, ...
- ex. 크기가 7인 해시테이블에서 해시 함수로 h(k)=k mod 7을 사욯한다고 가정, 8,1,9,6,13의 순으로 키 저장(오버플로우 발생하면 항목 저장을 위해 빈 버킷 순차적으로 탐색)

- 해시테이블은 1차원 배열로 구현. (키필드와 키와 관련된 자료필드 가짐)
- 여기서는 키가 문자열로 되어있다고 가정, 버킷당 하나의 슬롯 가정

- 해시 테이블의 각 요소들은 초기화과정 거쳐야 함. (각 버킷들을 공백상태로 만드는 것)
- 문자열이 키이므로 키의 첫번째문자가 NULL값이면 버킷이 비어있는 걸로 생각할 수 O
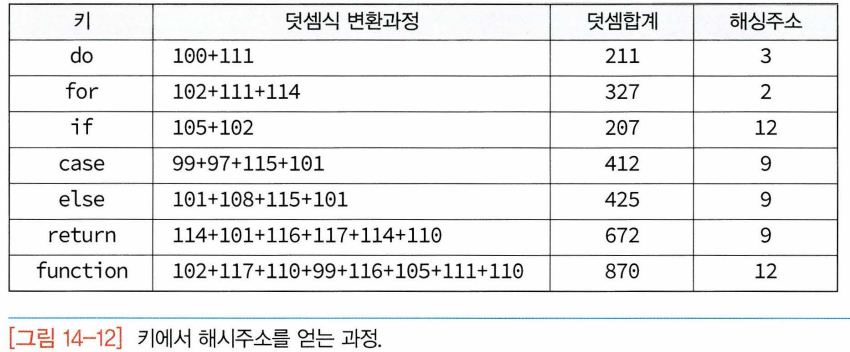
- 충돌이 일어나는 'case', 'else' , 'return'/'if', 'function' 은 모두 같은 해시주소로 계산. ->선형조사법으로 해결가능
- 원형으로 회전함을 기억해야 함. 테이블의 마지막에 도달하면 다시 처음으로 감.
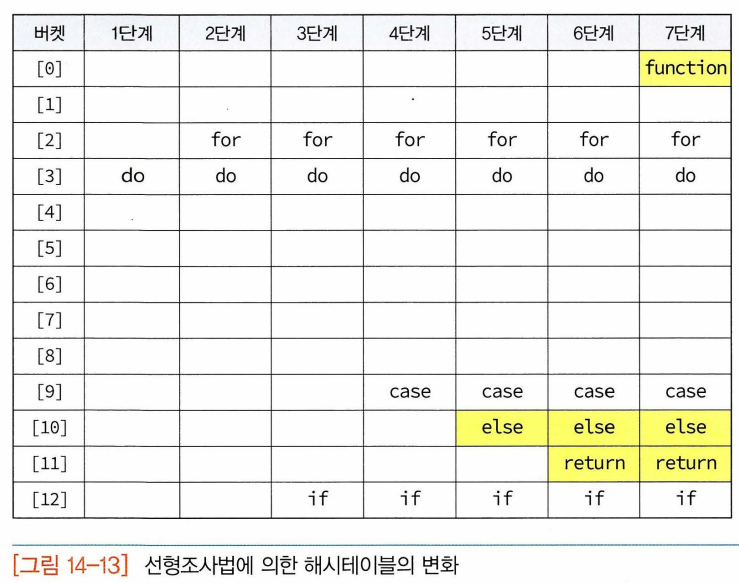
- 군집화: 한 번 충돌이 시작되면 그 위치에 항목 집중
- 선형조사법의 장점: 간단
- "의 단점: 키들이 집중되어 저장되는 현상 발생, 최악의 경우에 집중된 항목들이 결합하는 현상까지 발생 -> 탐색시간이 길어짐. 오버플로우가 자주 발생하면 집중과 결합에 의해 탐색의 효율이 크게 저하될 수 있음
- 선형조사법에서 항목이 삭제되면 탐색이 불가능해질 수 o. 크기가 10인 해시테이블과 h(k)=k mod 10인 해시함수 가정

- 삭제가 가능하게 하려면 버킷을 한 번도 사용 안 된 버킷, 사용됐으나 현재는 비어있는 버킷, 현재 사용중인 버킷으로 분류해야 함. 탐색함수에서 한 번도 사용이 안 된 버킷을 만나야만 탐색이 중단되도록 해야 함.
이차 조사법
- 선형조사법과 유사
- 조사할 위치를 이 식에 의해 결정 : (h(k)+inc*inc) mod M for inc=O,l , ... ,M-1
- 조사되는 위치: h(k), h(k) + 1, h(k) +4, h(k) +9, ...
- 모든 위치를 조사하게 만들려면 여전히 테이블 크기는 소수여야 한다.
- 선형조사법에서의 문제점인 집중과 결합을 크게 완화시킬 수 있음
- 2차집중문제를 일으킬 수 있지만 1차 집중처럼 심각한 것은 x
- 2차집중 이유: 동일한 위치로 사상되는 여러 키들이 같은 순서에 의해 빈버킷 조사하기 때문
- 이중해싱법으로 해결 가능
- 2차집중 이유: 동일한 위치로 사상되는 여러 키들이 같은 순서에 의해 빈버킷 조사하기 때문
- 2차집중문제를 일으킬 수 있지만 1차 집중처럼 심각한 것은 x
- 선형조사법에서의 문제점인 집중과 결합을 크게 완화시킬 수 있음
이중 해싱법
- 이중 해싱법(재해싱): 오버플로우가 발생함에 따라 항목을 저장할 다음 위치를 결정할 때 원래 해시 함수와 다른 별개의 해시 함수를 이용하는 방법
- 항목들을 해시 테이블에 보다 균일하게 분포 가능 -> 효과적인 방법
- 선형조사법, 이차조사법은 충돌이 발생했을 때 해시함수값에 어떤 값을 더해서 다음 위치 얻음(선형조사법: 1, 이차조사법: inc*inc)
- 해시함수값이 같으면 차후에 조사되는 위치도 같음
- 이중해싱법에서는 키를 참조하여 더해지는 값 결정. 따라서 해시 함수값이 같더라도 키가 다르면 서로 다른 조사순서 가짐. -> 이중해싱법은 이차집중 피할 수 o.
- 두번째 해시함수는 조사간격 결정. h'(k) = C-(k mod C) - 이런형태의 함수는 [l..C] 사이 값 생성.
- 충돌이 발생했을 경우 조사되는 위치 : h(k), h(k)+h'(k), h(k)+2*h'(k), h(k)+3*h'(k), ...
- C는 보통 테이블의 크기인 M보다 약간 작은 소수. 이중해싱에서는 같은 버킷과 같은 탐색 순서 갖는 요소 거의 없음 -> 보통 집중현상 매우 드묾
- ex. 크기가 7인 해시테이블에서 첫번째 해시 함수가 h(k)=k mod 7이고 오버플로우 발생시의 해시함수가 h'(k)=5-(k mod 5)일 때
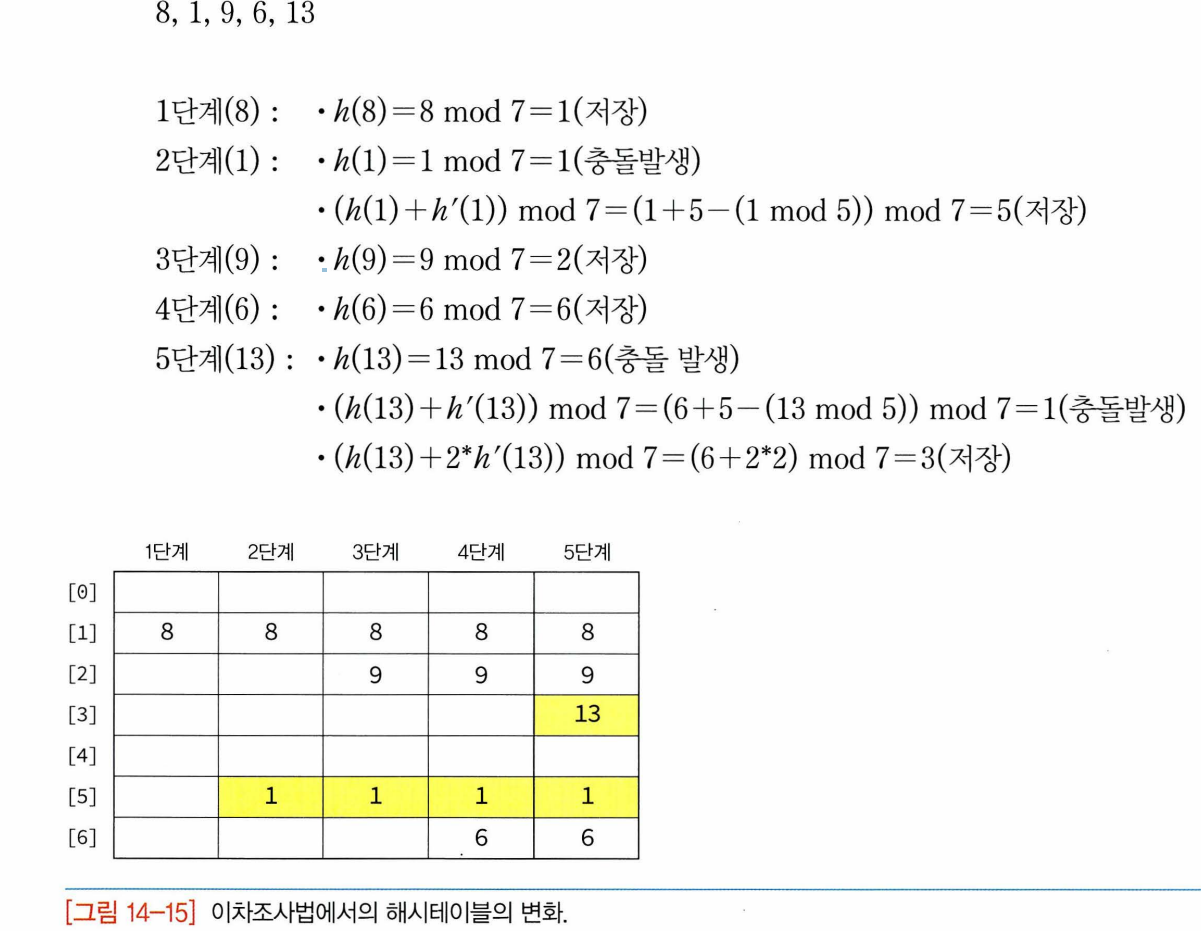
- 마지막 키인 13을 삽입할 때 키 13에 대해 해시함수 적용시키면

- 조사는 인덱스 6에서 시작, 2씩 증가.
- 한 가지 유의할 점 : 테이블의 끝에 도달하면 다시 처음으로 감. 조사가 되는 인덱스 나열하면 테이블의 모든 위치를 조사하게 됨(테이블 크기가 소수일 경우에만 적용)
- 테이블 크기를 6으로 바꾸면?

조사가 되는 위치 : 1,3,5,1,3,5 ... 가 돼서 같은 위치만 되풀이. -> 해시테이블의 크기는 소수가 돼야 함.
- 선형조사법의 문제점 : 한 번도 사용되지 않은 위치가 있어야만 탐색이 빨리 끝남. 만약 거의 모든 위치가 사용되고 있거나 사용된 적이 있는 위치라면 실패하는 탐색인 경우 ---> 테이블의 거의 모든 위치를 조사. -> 체이닝방법은 이러한 문제점 x
14.6 체이닝
- 선형조사법이 탐색시간이 많이 걸리는 이유: 충돌때문에 해시주소가 다른 키하고도 비교를 해야 함.
- 해시주소가 같은 키만을 하나의 리스트로 묶어둔다면 불필요한 비교 안 해도 됨.
- 리스트는 그 크기 예측 불가 -> 연결리스트로 구현하는 것이 가장 바람직
- 충돌을 해결하는 두 번째 방법: 해시테이블 구조를 변경하여 각 버킷이 하나 이상의 값 저장할 수 있도록 하기
- 해시주소가 같은 키만을 하나의 리스트로 묶어둔다면 불필요한 비교 안 해도 됨.
- 체이닝: 오버플로우 문제를 연결리스트로 해결 : 각 버킷에 고정된 슬롯을 할당하는 것이 아니라 각 버킷에 삽입과 삭제가 용이한 연결리스트 할당. 버킷 내에서는 원하는 항목 찾을 때 연결리스트 순차탐색.

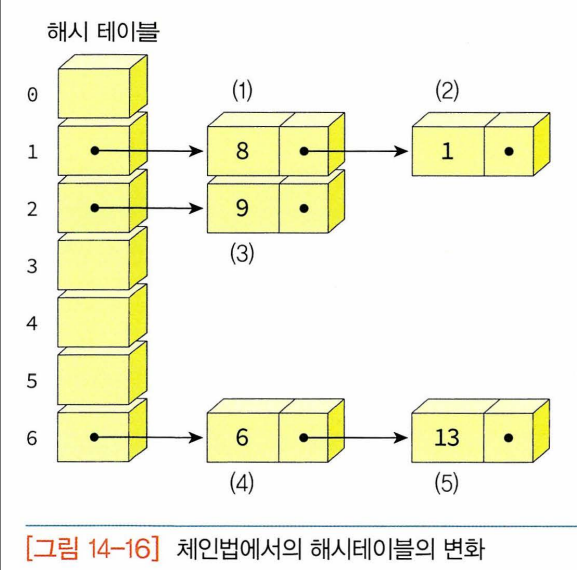
- 결정해야 할 것 : 연결리스트의 어디에 새로운 항목을 삽입하느냐.
- 키들의 중복을 허용한다면 연결리스트의 처음에 삽입하는 것이 가장 능률적.
- 중복 허용되지 않는다면 연결리스트를 처음부터 탐색해야 하므로 어차피 연결리스트의 뒤로 가야하고 여기에 삽입하는 것이 자연스러움
- 키들의 중복을 허용한다면 연결리스트의 처음에 삽입하는 것이 가장 능률적.
14.7 해싱의 성능분석
- 해싱에서 가장 중요한 연산 : 탐색연산 - 해시테이블에 자료 추가하거나 꺼내거나 삭제하는 연산들은 모두 사용
- 성공적인 탐색, 실패한 탐색 2가지로 나눠 생각하기
- 이상적 해싱함수: 시간복잡도-O(1) : 충돌이 전혀 일어나지 않는다는 가정 하에서만 가능
- 일반적으로는 충돌이 있다고 가정 -> 얘보단 느려짐
- 해시테이블의 적재밀도(적재비율) : 해시테이블이 얼마나 채워져 있는지 나타내는 하나의 척도(해싱의 성능 분석 위해)
- 저장되는 항목 개수 n과 해시테이블의 크기 M의 비율

- a가 0이면 해시테이블은 비어있음. a의 최대값은 충돌 해결 방법에 따라 달라짐
- 선형조사법에서는 해시테이블이 가득 찬다면 각 버킷당 하나의 항목 저장->1
- 체인법에서는 저장할 수 있는 항목의 수가 해시테이블의 크기 넘어설 수 있음 -> a는 최대값 갖지 x.
- 선형조사법에서는 해시테이블이 채워지면 충돌이 더 자주 일어남. 탐색을 위한 비교연산의 개수

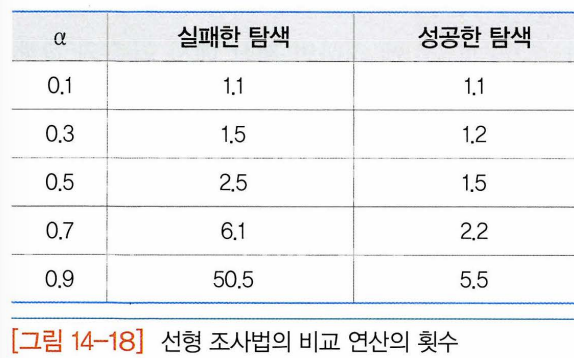
- 위 수식을 이용해 몇 개 a값에 대해 테이블을 만들어보면 ,
- 해시 테이블이 절반정도 채워진 상태에서는 실패한 탐색은 2.5 비교연산 요구
- 성공한 탐색의 경우 1.5비교연산 요구
- a가 0.5 넘어갈수록 실패한 탐색은 급격히 탐색시간 증가.
- 결론적으로 해시 테이블의 적재밀도가 0.5를 넘어가지 않도록 해야 한다.
- 체이닝방법에서 a=항목의 개수/연결리스트의 개수로 나눈 것(a는 평균적으로 하나의 연결리스트당 몇개의 항목 갖고 있냐)
- 실패하는 탐색: 찾고자 하는 위치에 연결리스트가 비어있다면 O(1)의 시간만 걸림, 하지만 평균적인 경우 a만큼의 항목 탐색해야 함.
- 성공적인 탐색의 경우 : 항상 연결리스트에 항목 존재해야 함, 평균적으로 a의 항목 비교해야 함, 테이블에 존재하는 포인터까지를 계산에 넣는다면 1+a/2가 됨

- 체인닝의 경우 a가 증가하더라도 성능이 급격히 떨어지지는 x. 효율성을 위해서는 a를 유지할 필요 o
- 제산해시햄수와 함께 체이닝 사용하는 방법이 가장 효과적
[해싱 정리]
- 선형조사법 : 적재밀도를 0.5이하로 유지
- 이차조사법, 이중해싱법 : 적재밀도를 0.7이하로 유지
- 선형조사법은 테이블 크기에 따라 저장할 수 있는 요소들의 개수에 자연적 제한
- 적재밀도가 작은 경우 이차조사법이나 이중해싱보다 효율적일 수 O

- 체인법은 적재밀도에 비례하는 성능보임. 성능 저하시키지 않고 얼마든지 저장할 수 있는 요소 개수를 늘릴 수 있다는 것이 장점. 링크 위한 메모리 낭비 문제는 저장되는 자료 크기 따라 달라짐
- 해싱을 배열이용하는 이진탐색과 비교해보면 해싱이 일반적으로 빠름. 삽입이 어려운 이진탐색과 달리 삽입 쉬움.
- 해싱을 이진탐색트리와 비교해보면 이진탐색트리는 현재값보다 다음으로 큰값이나 다음으로 작은값 쉽게 찾을 수 있는 장점 있음, 값의 크기순으로 순회하는 것이 쉬움
- 하지만 해싱은 순서 없고 해시 테이블에 초기에 얼마나 공간을 할당해야 하는지 불명확, 최악의 시간복잡도는 아주 나쁨. 최악의 경우 : 모든 값이 하나의 버킷으로 집중 - 시간복잡도 :O(n)

'CS > 자료구조' 카테고리의 다른 글
| [자료구조] ch13. 탐색 (3) | 2024.11.25 |
|---|---|
| [자료구조] chap12. 정렬 (0) | 2024.11.19 |
| [자료구조] chap11. 그래프 II (1) | 2024.11.12 |
| [자료구조] chap10. 그래프 I (4) | 2024.11.05 |
| [자료구조] chap9. 우선순위 큐 (0) | 2024.10.22 |