1. 만유인력
- 브라헤 : 20년에 걸친 방대한 정밀 천문 관측(태양계 행성, 별 777개)
- 케플러: 16년동안 브라헤의 관측자료로 행성 운동 설명할 수 있는 수학적 모형 추론, 원궤도 개념 탈피, 타원궤도 개념 도입. -> "케플러의 행성운동 법칙"
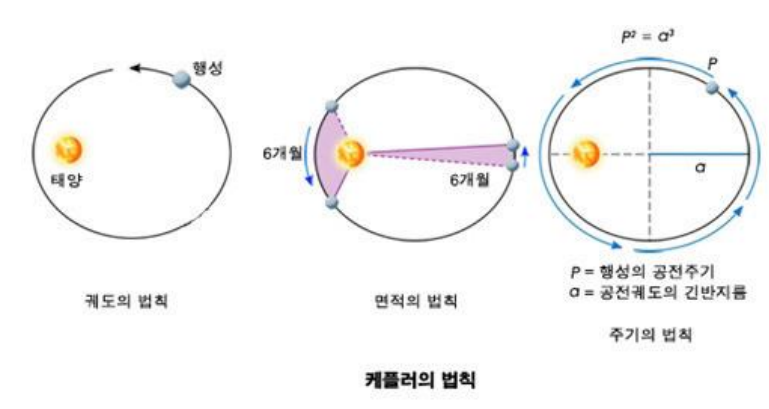
- 뉴턴: 달의 운동은 직선운동이 아닌 "타원궤도 운동" -> 인력(구심력), 태양계행성과 모든 물체 간 작용하는 일반적이고 보편적인 힘 => 만유인력 법칙(행성의 운동을 매우 만족스럽게 설명)
<케플러 행성의 세 운동 법칙>
*만유인력의 법칙 유도 가능
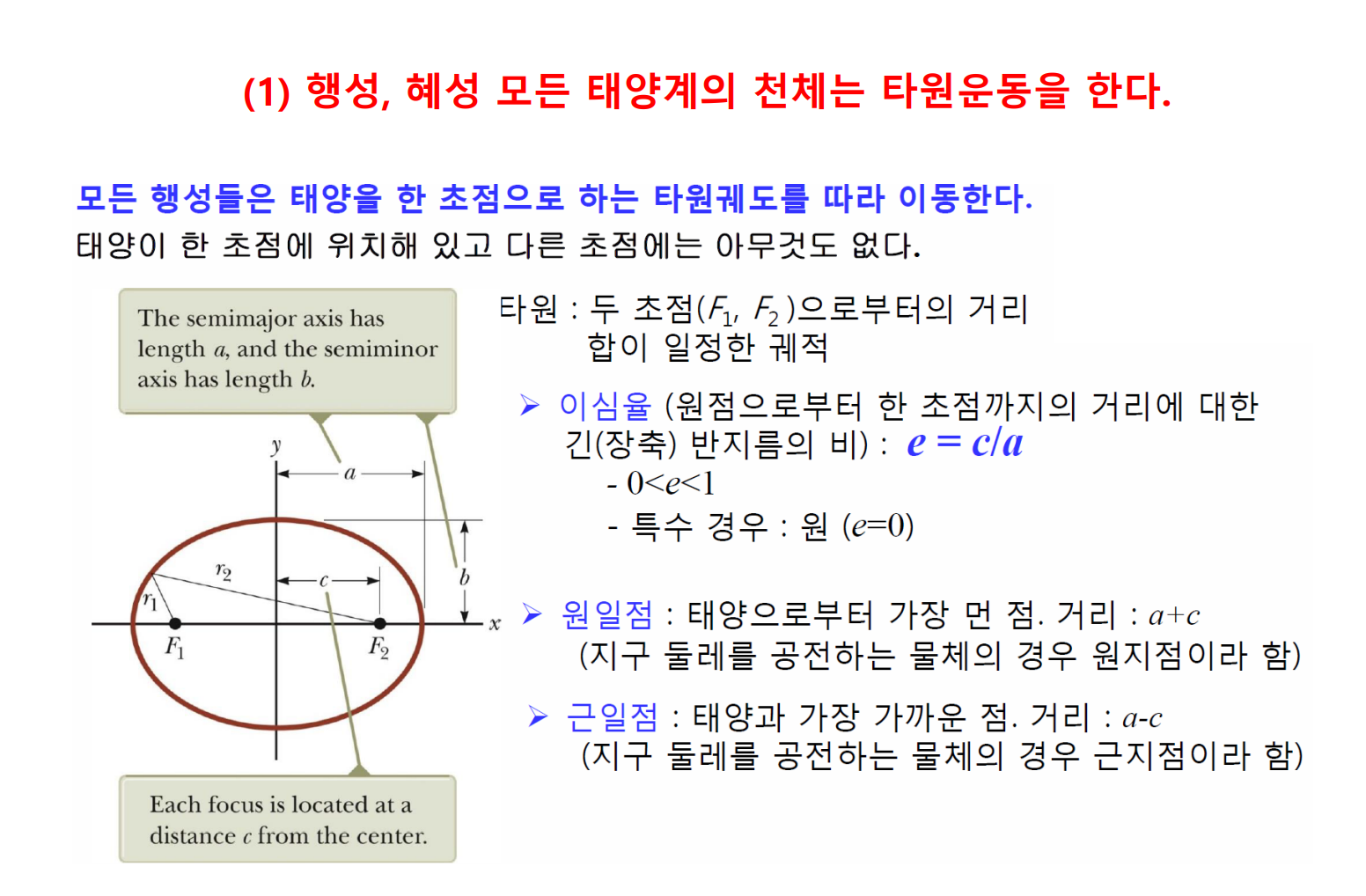
- 이심률 e : 행성들의 궤도가 납작한 정도

*L : 각운동량 | r: 물체와 중심체 사이의 거리 | p: 선운동량 | Mp: 중심체 주변을 공전하는 행성이나 위성과 같은 물체의 질량 | v: 속도
* L=r⋅p -> 각운동량= 위치 벡터 와 선운동량 의 벡터곱
*
- 행성과 태양을 연결한 직선은 같은 시간에 같은 면적을 쓸고 지나감 : 행성의 공전속도가 태양에 가까워지면 빨라지게 되고 멀어지면 느려지기 때문에!

* : 뉴턴의 제2법칙 : 뉴턴의 운동 법칙에 따라, 물체에 작용하는 힘(중력, 만유인력) Fg는 물체의 질량 와 가속도 a의 곱.
- : 중심체(예: 태양)의 질량
- Mp: 궤도 위 물체(예: 행성)의 질량
- G: 만유인력 상수
- r: 두 물체 사이의 거리
- 중력가속도 : a=v^2/r
* 원심력 Fc=Mpv^2 / r : 궤도 운동
궤도를 따라 움직이는 물체는 원심력과 중심체의 중력이 평형을 이루어야 하므로: Fg=Fc
* 케플러 제3법칙은 궤도의 반지름과 공전 주기 T 사이의 관계를 나타낸다.
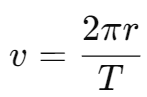

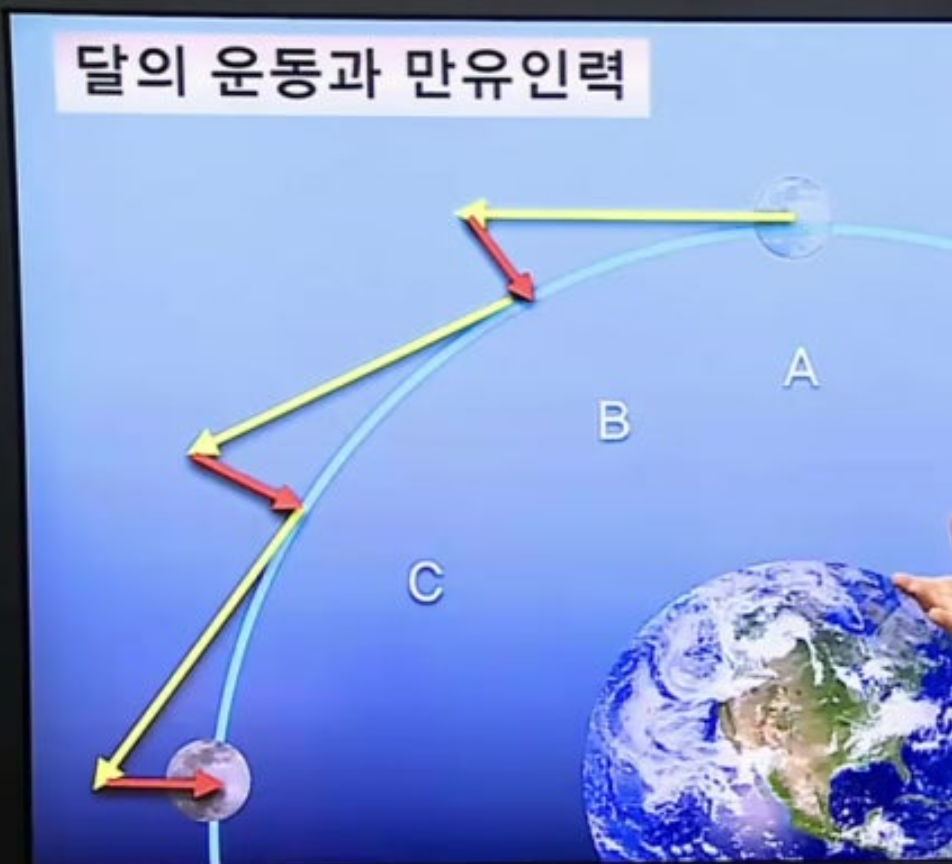
- 뉴턴의 만유인력 법칙 : 행성이 왜 위와 같은 행동을 하는가?
- 우주에 존재하는(질량이 있는) 두 입자 사이에는, 두 입자의 질량의 곱에 비례하고 이들 사이 거리의 제곱에 반비례하는 인력이 작용.
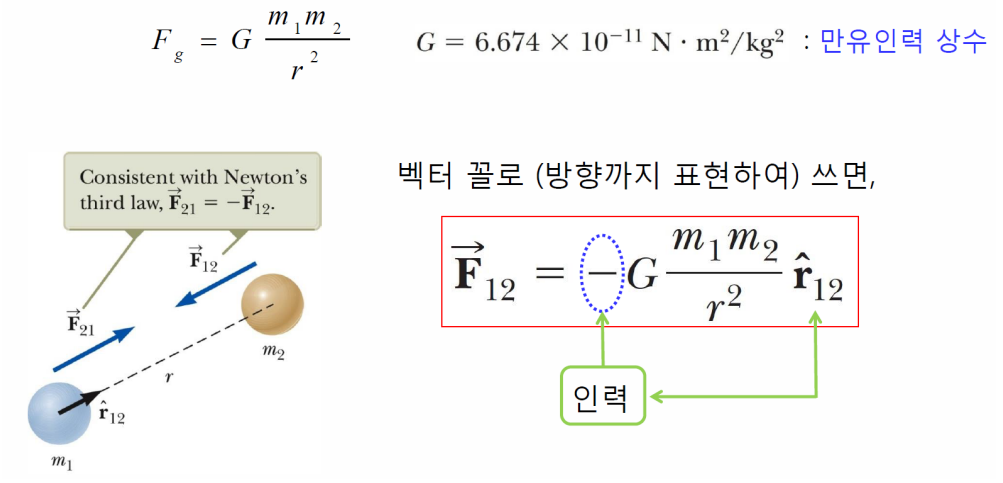
- 구심력과 원심력




- 만유인력 상수의 측정

- 두 질량 M,m 사이의 인력에 의해 막대 회전
- 줄이 꼬이면서 거울 회전
- 거울에 입사한 빛의 반사각도 변화
- 막대의 회전 정도로부터 힘 측정
- 질량 M과 거리 r 바꿔가며 주의깊게 반복측정(거리, 줄의 비틀림 탄성도, 질량들의 크기...)
- 만유인력 상수의 특이점
- 기본전하나 전자질량과 같은 다른 기본상수보다도 측정 불확정도가 수천배 이상 높음 > 아직까지 활발하게 연구.
- (지표면) 중력장 vs 만유인력: 중력이 '장(field)'를 통해 두 단계 과정을 거쳐 발생하는 것으로 고려:


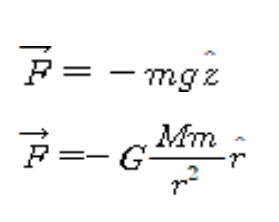

2. 인공위성
- 정지위성 :
- Q. 지표면으로터 고도 h에서 지구 주위를 일정한 속력 v로 원운동하고 있는 질량 m인 위성이 있다.


* 지구정지궤도 : 인공위성이 지구의 자전과 동일한 속도로 회전하며, 따라서 지구 상의 특정 지점에 대해 항상 고정되어 있는 것처럼 보인다. 위성의 회전 주기는 지구의 자전 주기와 동일.




- 탈출속도
- 지구나 다른 천체의 중력을 이겨내고 해당 천체를 벗어나 우주로 탈출하기 위한 최소속도(물체가 천체의 중력장 밖으로 나가는 데 필요한 최소속도) - 중력의 잠재적 에너지와 물체의 운동에너지가 같을 때 얻어진다.
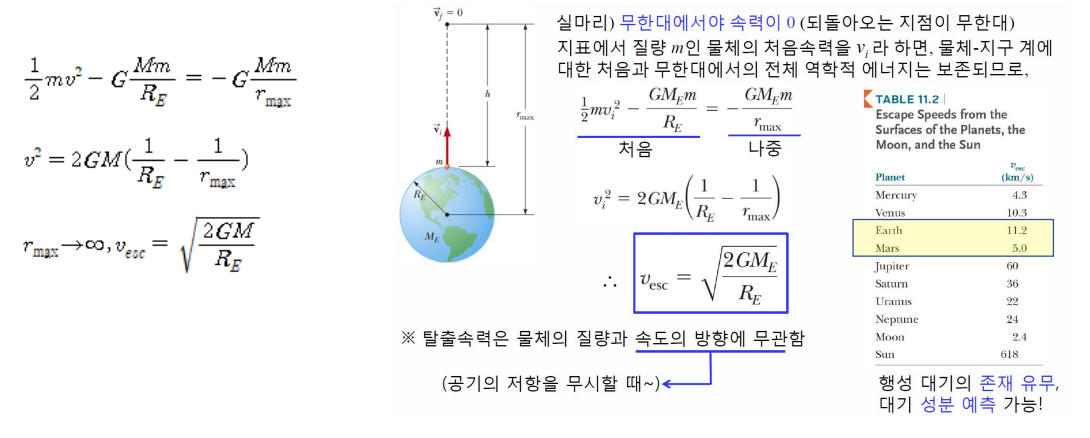



3. 진동
*진동파동음파 중에 2문제 나옴
* 시험 : 기타의 줄의 굵기 다름
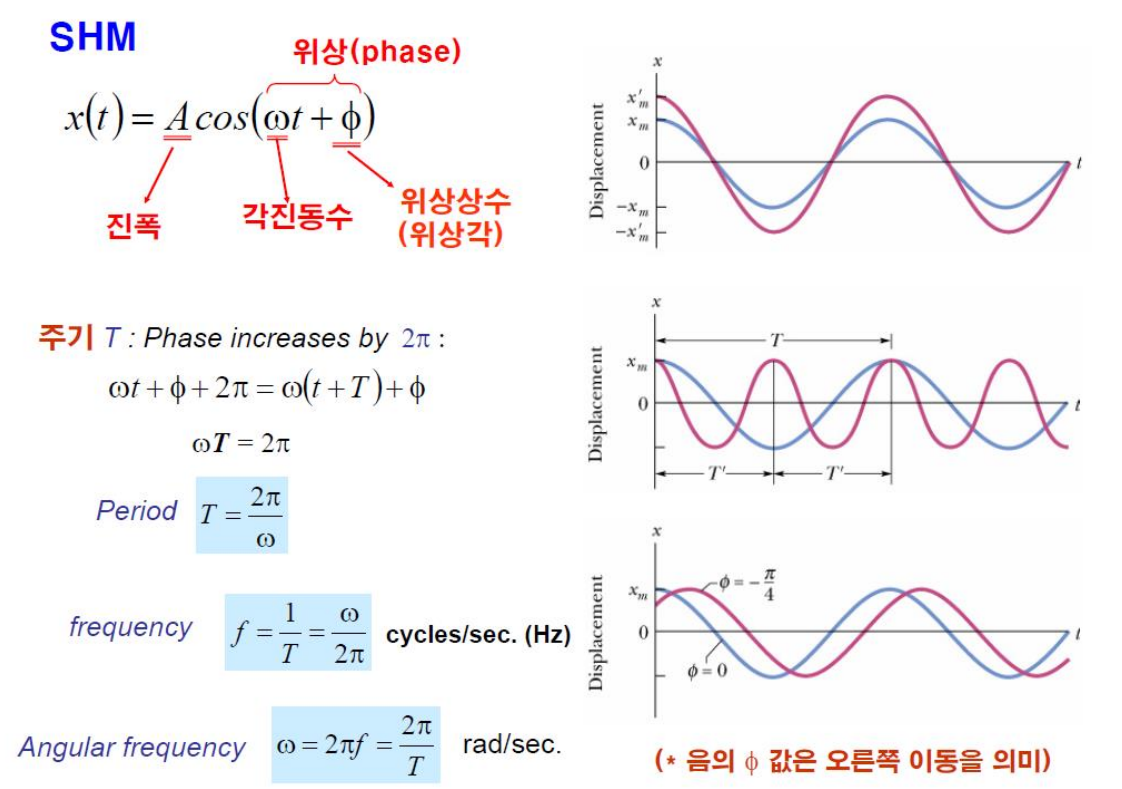
1) 단순 조화 운동
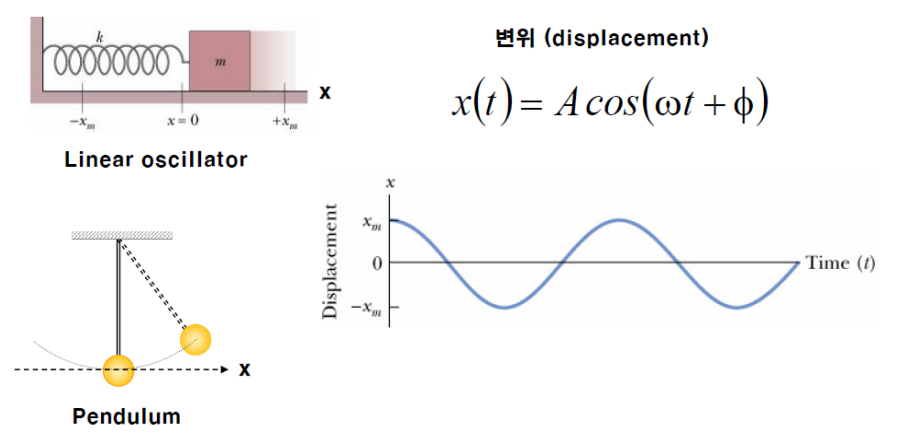
: 물체의 위치가 시간에 대한 조화함수로 기술되는 운동
일정한 주기로 반복되는 주기적인 운동으로, 주로 힘이 물체를 원위치로 되돌리려는 복원력에 의해 발생한다. 이 운동은 여러 물리적 시스템에서 관찰될 수 있으며, 진자나 스프링과 같은 시스템에서 흔히 나타난다.
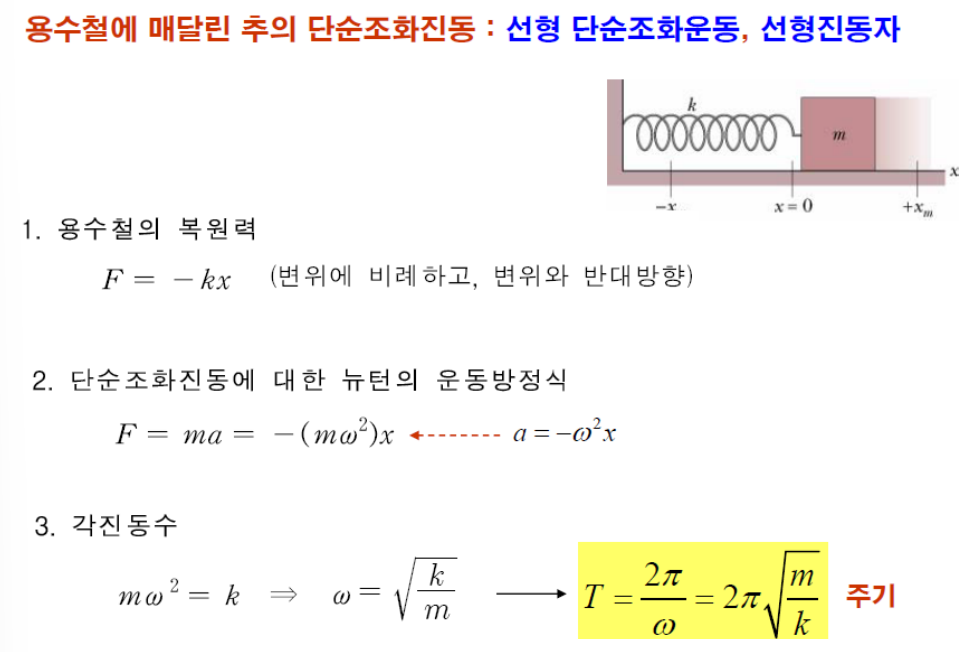
- 복원력은 물체의 변위에 비례하고, 반대 방향으로 작용한다. 즉, 물체가 원위치에서 멀어질수록 복원력은 더 커진다.
- : 복원력 (N)
- : 스프링 상수 (N/m), 또는 물체에 작용하는 복원력의 강도
- : 물체의 변위 (m), 원위치로부터의 거리
- 부호 −는 복원력이 변위의 반대 방향으로 작용함을 나타낸다.




2)선형진동자
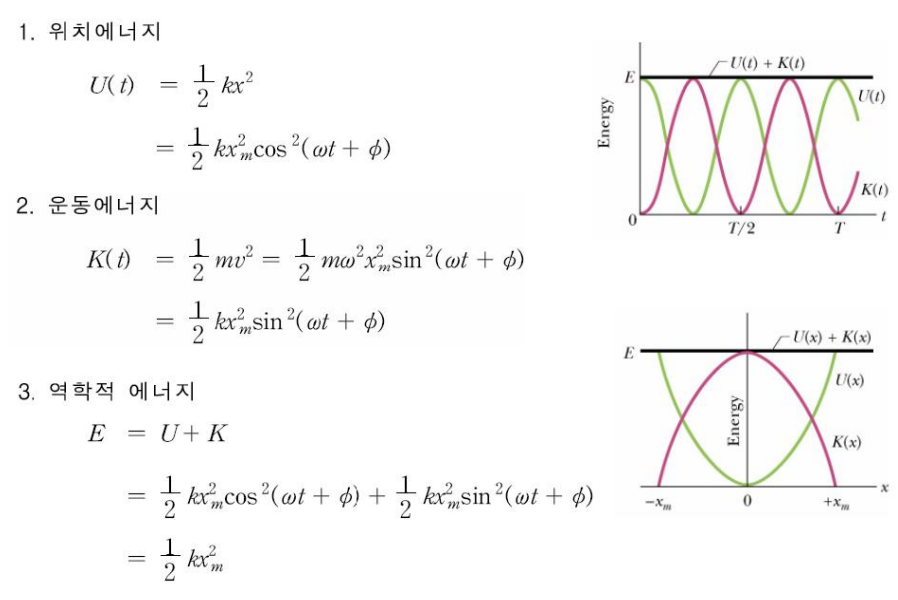




3) 진자(하이라이트)
- 진자의 운동은 중력과 줄의 장력에 의해 이루어짐
- 추의 질량: m, 줄길이 L, 진자가 회전 중심에서 각도 만큼 기울어져 있다고 가정. 진자가 움직이는 궤적은 원형이며 원형호의 길이 s는 각도 θ와 줄의 길이 L에 따라 s=Lθ 같은 관계를 가짐
- 중력 mg는 법선방향(줄의 방향, 장력과 상쇄되며 줄의 장력 조절 가능)과 접선방향(진자의 운동에 영향 주는 힘)으로 분해될 수 있음
- F : 힘은 접선 방향으로 작용, 이는 진자를 원점(균형위치)로 되돌리려는 복원력, 크기는 s에 비례.
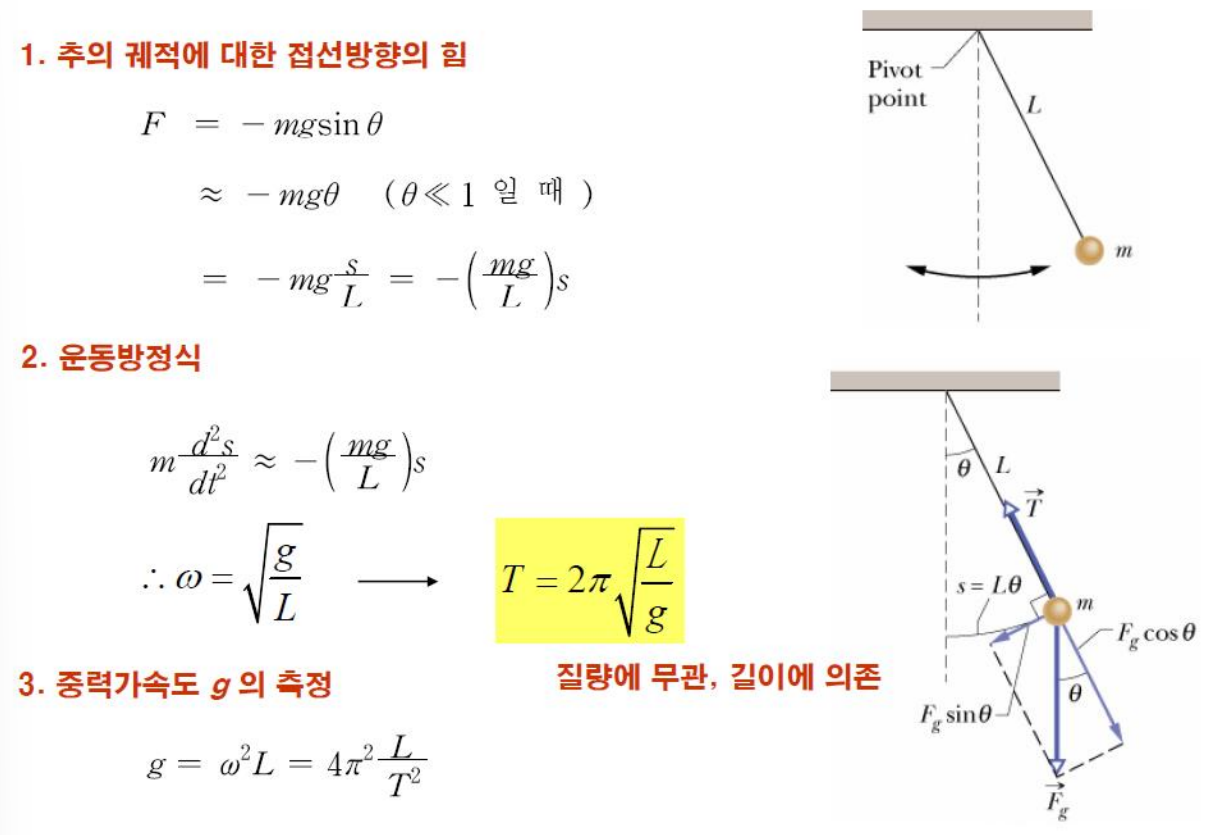
- F=ma에서 a는 가속도.
- 접선방향의 힘 -mgsinθ 에서 -부호는 힘이 진자 운동의 반대방향으로 작용함 의미
- 각진동수 w 대입하고 주기(T)에 대한 식으로 정리하면 T=2π/w 에서 위 식 나옴
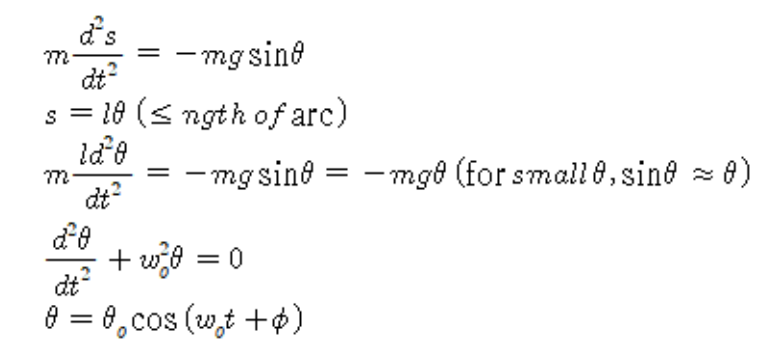
- : 최대 진폭(초기 각도).
- ω0= 루트(g/L): 고유 각진동수.
- : 초기 위상, 에서의 초기 위치를 결정.
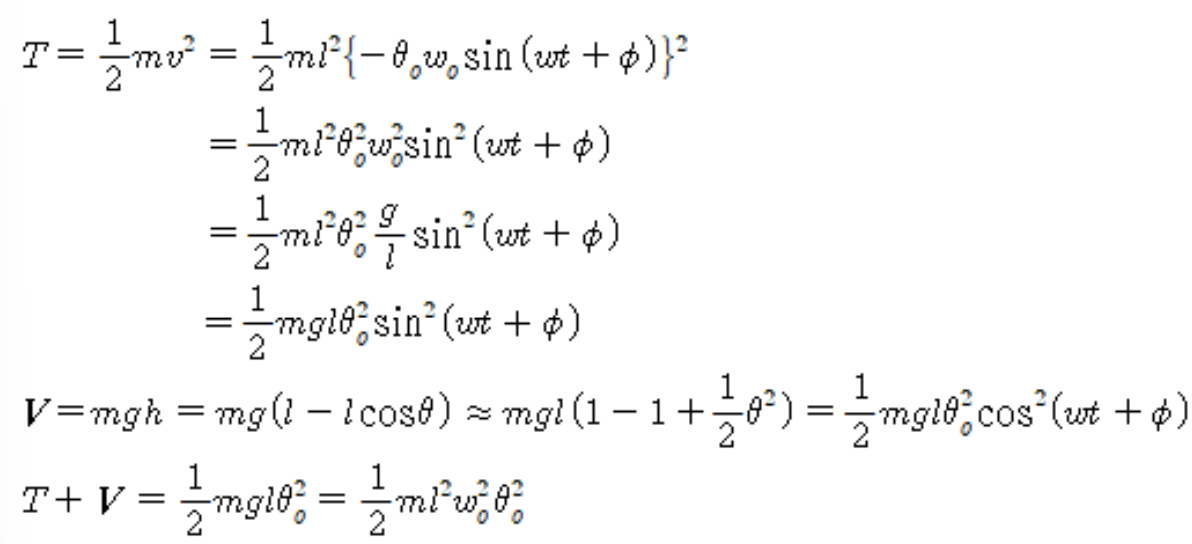
- 운동에너지 T: 진자가 움직이면서 갖는 에너지. 진자의 속도 v는 줄의 길이 l과 각속도 v=l θ˙로 나타낼 수 있음, θ˙=−θ0ω0sin(ω0t+ϕ)는 각운동의 미분
- mgh=진자의 위치에너지, 높이 h를 줄의 길이 L과 각도 θ 이용해 표현.

[예제]
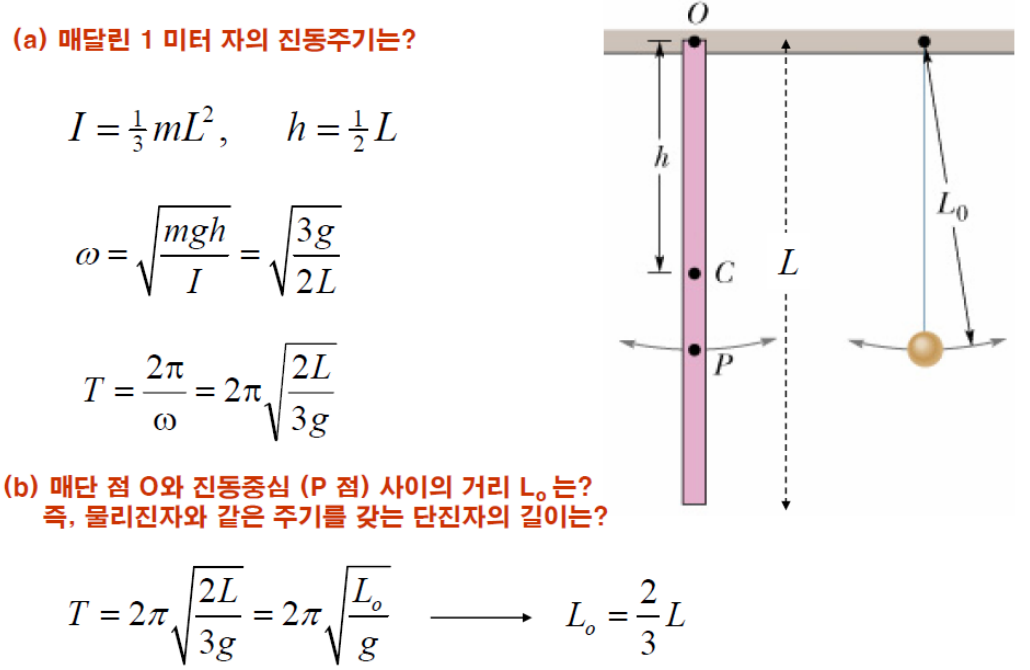
- 단진자 : 이상적인 진자모델, 질량이 없는 줄에 질량이 집중된 물체가 매달려 진동하는 시스템. 진자가 진동하는 동안 줄이 일정하게 늘어나지 않고 질량은 단 한 점에 집중돼있다고 가정
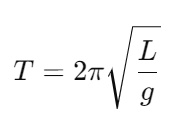
- 물리진자: 모든 질량이 일정하게 분포된 물체가 회전하는 진자 시스템, 단순한 질점이 아니라 회전축을 기준으로 질량이 분포된 물체가 진동- 실제진자운동 더 잘 설명
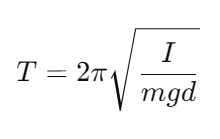
4) 감쇠진동
- 진동하는 시스템에서 시간이 지남에 따라 진폭이 점차 감소하는 진동현상 : 시스템이 에너지를 소산시키기 때문에 발생 (저항력, 마찰력 등 외부요인에 의해 발생)
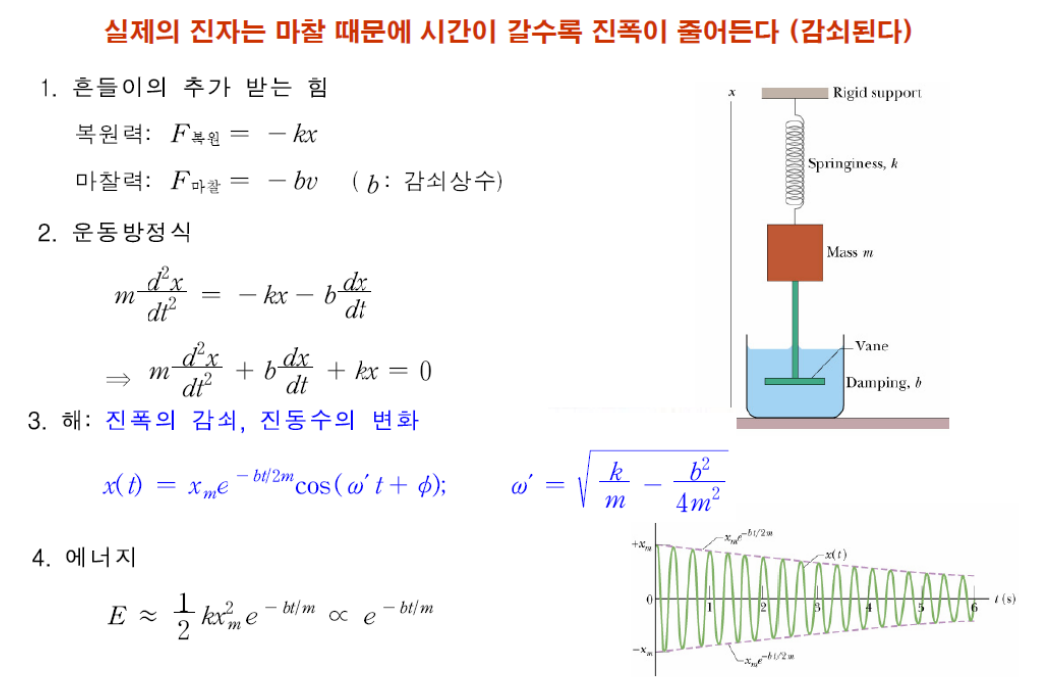
- 복원력 + 마찰력 = 물체에 작용하는 총 힘
감쇠진동과 강제진동
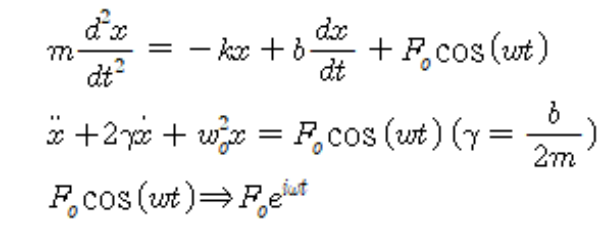
외력 X
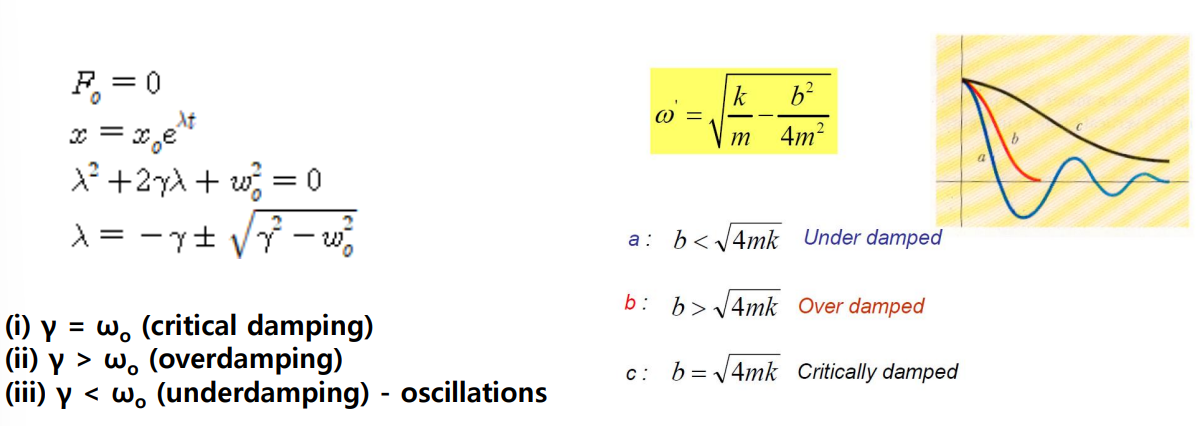
외력

4. 파동
| 진동 | 파동 |
| 에너지전달x | 에너지전달o |
| 횡파(빛), 종파(음파), 물결파, 포논 | |
| 주기, 진동수, 진폭 | 파장, 주기, 주파수, 진폭 |

- y(x,t): 위치 x와 시간 t에서의 파동의 변위
- ym: 파동의 진폭
- k: 파수(파장의 역수, k= 2π/ λ)
- 각진동수(ω=2π는 주파수)
- 파장(파동이 한 주기를 완성하는 거리)
- t: 시간
- 초기 위상
파동의 수학적 기술(파동방정식)
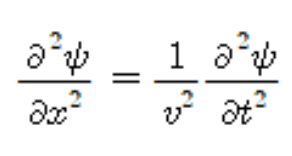
- 파동이 어떻게 전파되는 가에 대한 정보 제공
- 첫번째항 : 공간에서 두 번째 미분, 파동이 공간을 따라 어떻게 구부러지는지, 혹은 파동의 곡률 나타냄. 파동이 얼마나 퍼져나가는지, 수축하는지와 관련
- 두번째항: 파동이 이동하는 속도와 관련. v는 파동의 전파속도, 파동의 속도가 커질수록 파동의 시간적 변화에 비해 공간적 변화가 적게 일어남.
- 마지막항: 시간에 대한 두번째 미분. 파동의 가속도, 시간에 따라 파동이 어떻게 진동하는지(주기의 변화)와 관련.

- 역학적파동: 매질의존적(물질이 있어야만 발생전파)- 소리파는 공기나 물과 같은 매질 통해 전달
- 전자기파 : 전기장과 자기장의 변화가 서로 영향미쳐 발생, 물질 없어도 공간 통해서 전파
- 물질파 : 물질입자의 움직임에 의해 발생하는 파동, 양자역학에 의해 설명, 물질 입자가 파동처럼 행동하는 파동-입자 이중성 나타내는 중요한 개념
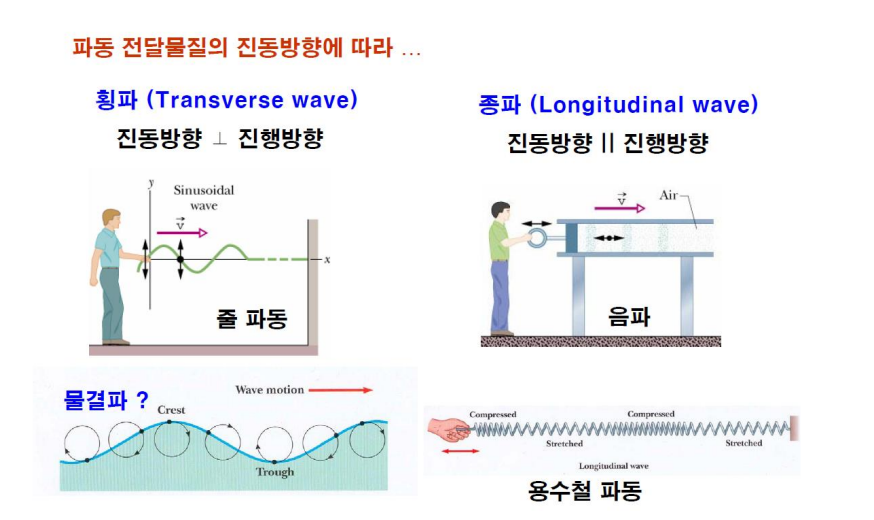
진동방향 y축, 진행방향 +x축인 진행파동함수

진동방향 y축, 진행방향 -x축인 파동함수
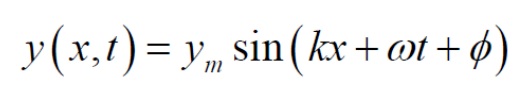
- w(각진동수): 파동이나 진동의 주파수를 각도로 표현한 값.(2πf)
- 진행방향이 반대로 바뀌면 파동은 반대방향으로 이동하게 되므로
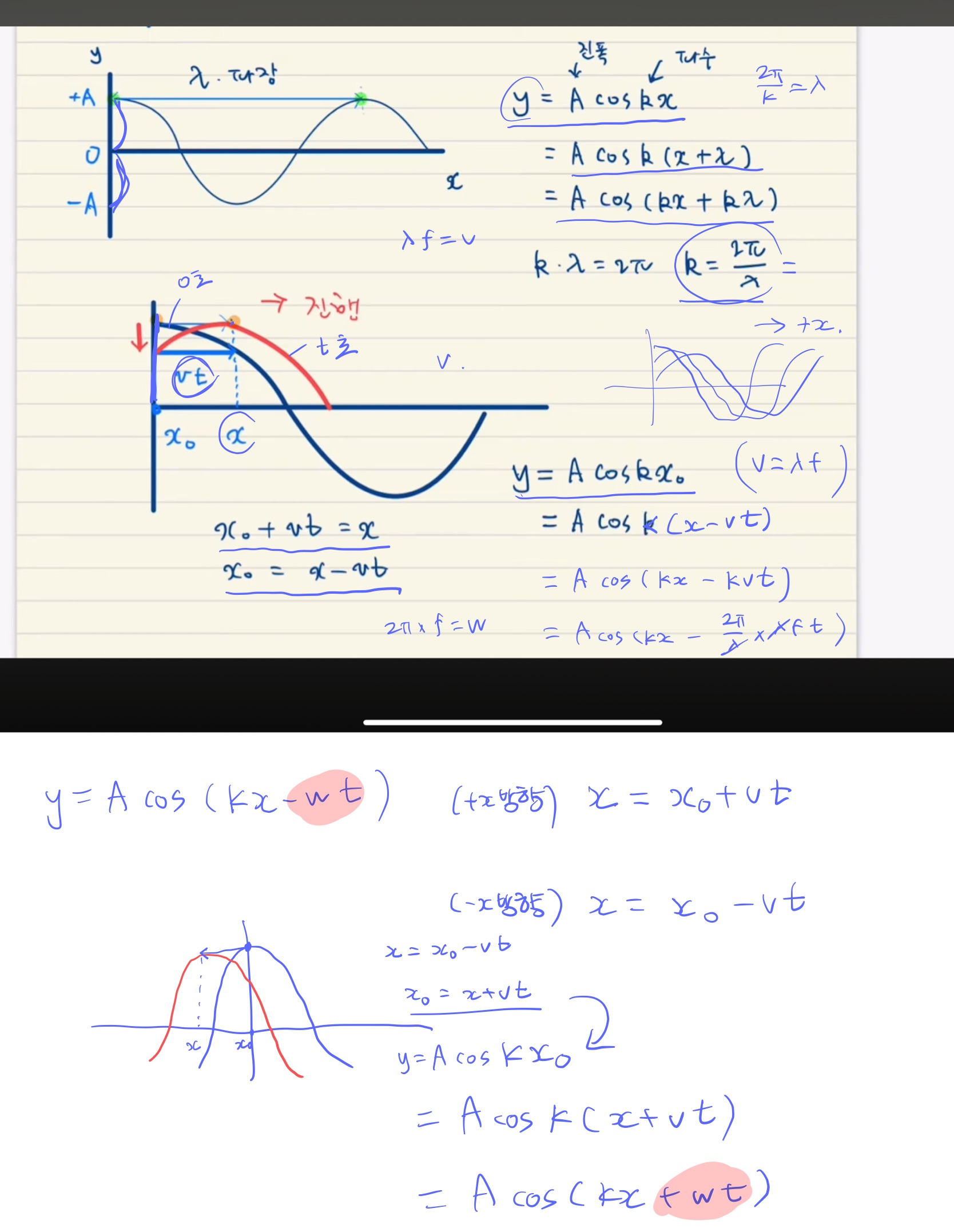
일반적인 진행파동 함수
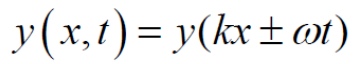
- y는 진동형태 나타내는 함수.
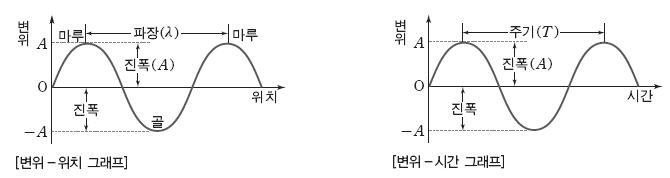
공간적 측면(파장과 각파동수) <------> 시간적 측면(주기와 각진동수)
- 파장: 파동이 한 번의 진동주기를 거쳐 전달되는 거리. 파동의 두 점에서 같은 위상에 있는 두 점 사이의 거리 의미
- λ(람다)로 나타내며, 단위는 주로 미터(m)를 사용
- 주기: 파동이 한 번의 진동을 완료하는 데 걸리는 시간, 파동이 한 사이클을 완료하는 데 소요되는 시간.
- T로 나타내며 단위는 초.
- 진동의 반복성이 시간에 따라 어떻게 이루어지는지를 나타냄
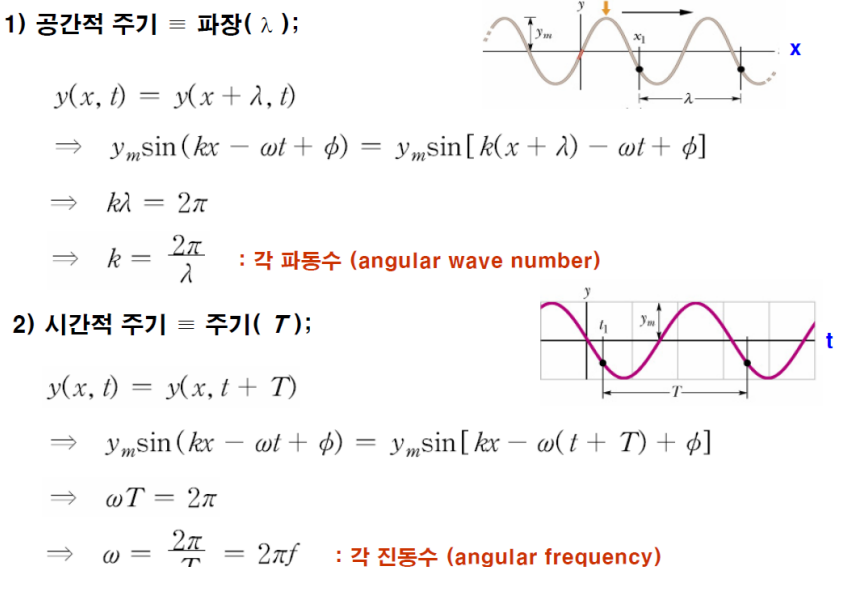
군속도 vs 위상속도
- 위상: 파동에서 특정한 시간과 공간에서의 진동 상태를 나타내는 개념입니다. 간단히 말해, 파동이 얼마나 진행되었는지 또는 어느 단계에 있는지를 나타내는 값입니다.
- 수학적으로, 위상은 ϕ(x,t)=kx−ωt+ϕ0로 표현됩니다.
- kx: 공간에서의 변화(파수 k와 위치 x에 따라 진동이 달라짐)
- ωt: 시간에 따른 변화(각속도 ω와 시간 )
- ϕ0: 초기 위상(파동의 시작 위치를 설정하는 값)
- 위상속도: 파동의 개별 위상이 이동하는 속도
- 계산식: vp=ω/k
- ω: 각진동수
- k: 파수
- 예를 들어, sin(kx−ωt)형태의 파동을 보면, 위상 ϕ=kx−ωt가 일정한 위치를 기준으로 이동하는 속도를 위상속도라고 합니다.
- 계산식: vp=ω/k
- 군속도: 파동군, 에너지나 정보가 전달되는 속도
- 계산식: vg=dω/dk
줄의 파동



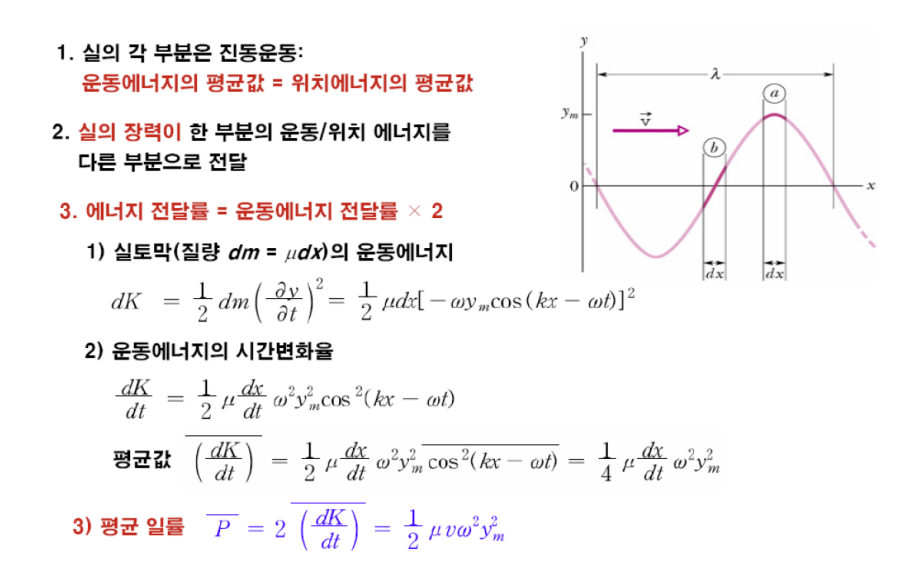
줄의 장력과 파동의 속도
*줄의 파동 : 시험에 나옴
선밀도: 질량/길이
장력=N(뉴튼)
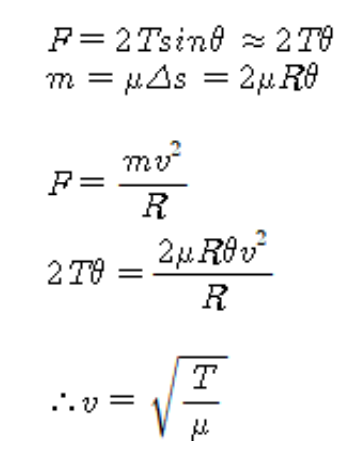


- v^2/R = 구심가속도

파동의 에너지 전달과 일률
- 운동에너지+위치에너지 = 역학적에너지
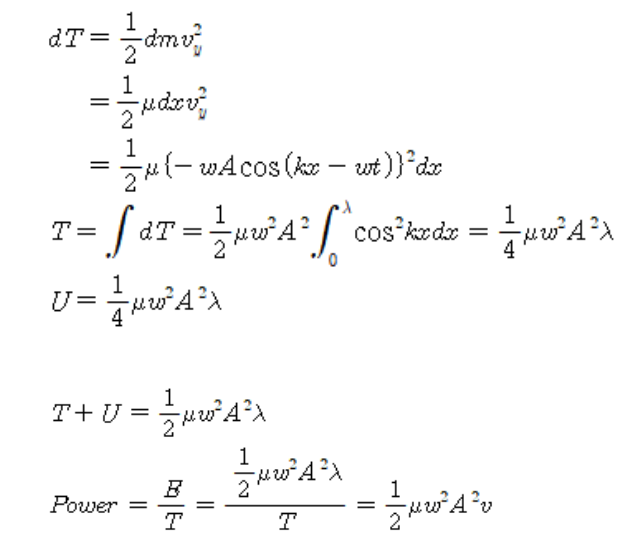

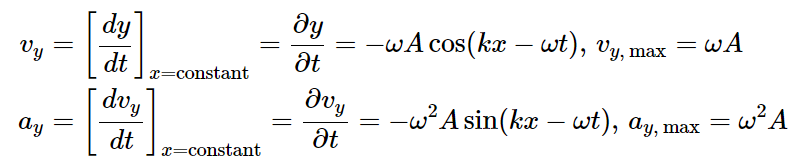
파동의 중첩
<참고블로그>
https://gooseskin.tistory.com/233
파동의 간섭(중첩과 독립성, 정상파, 영의 이중 슬릿 실험)
2021.11.10 - [2021 물리학1] - 전반사와 광통신 전반사와 광통신 2021.11.08 - [2021 물리학1] - 파동의 굴절과 생각의 왜곡 (스넬의 법칙, 신기루) 파동의 굴절과 생각의 왜곡 (스넬의 법칙, 신기루) 2021.10.28
gooseskin.tistory.com


파동의 간섭


* 파동=진폭항*파동항
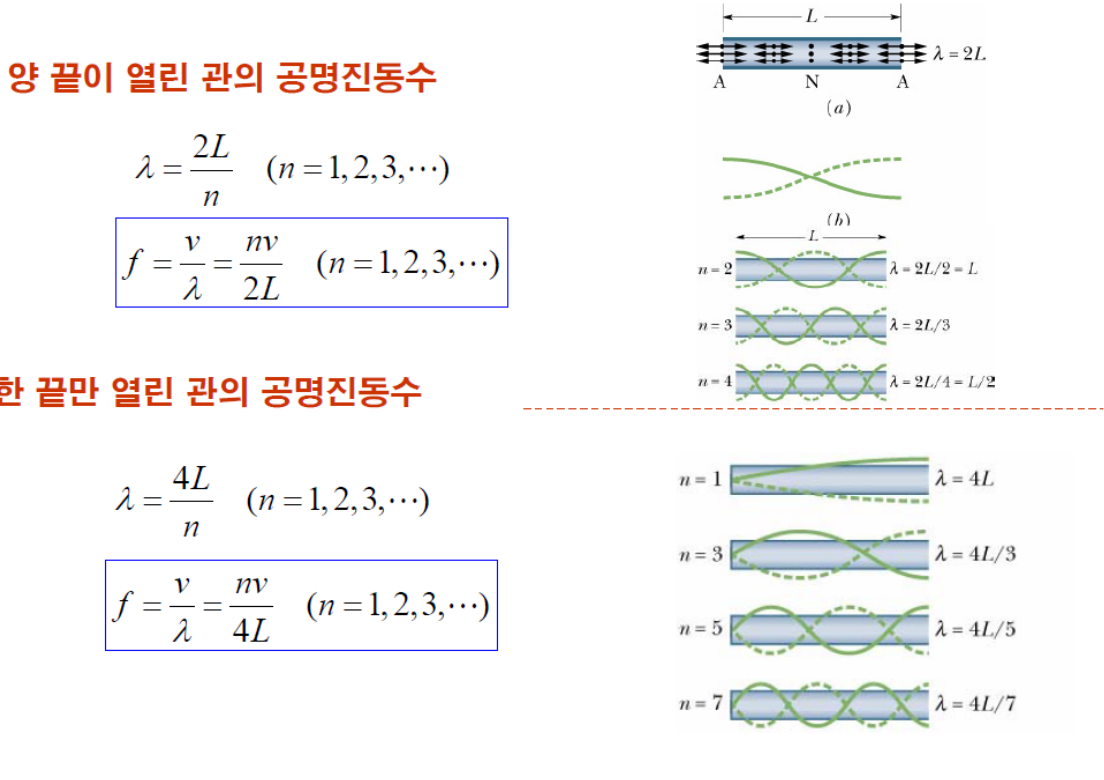
정지파
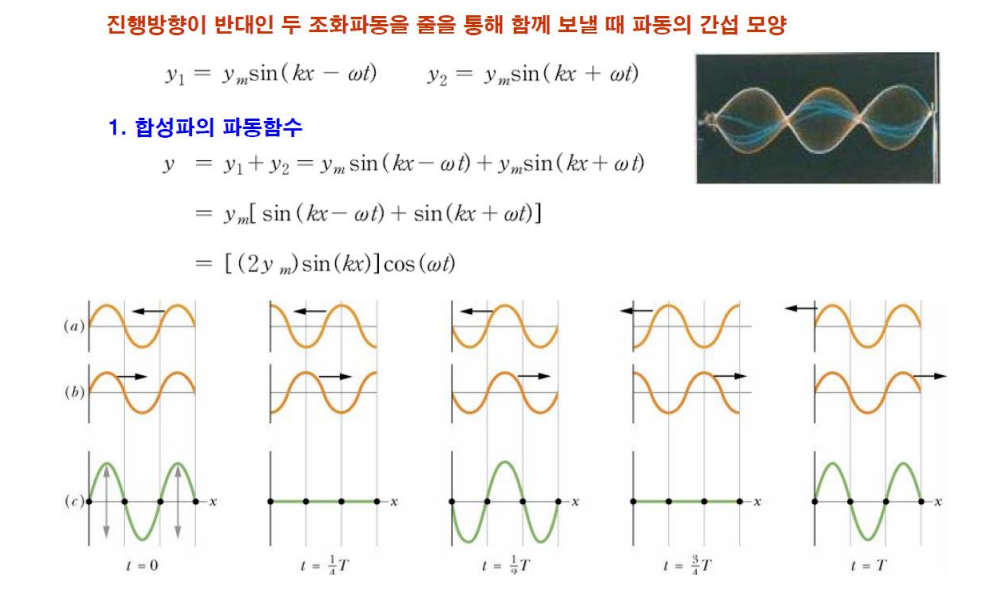

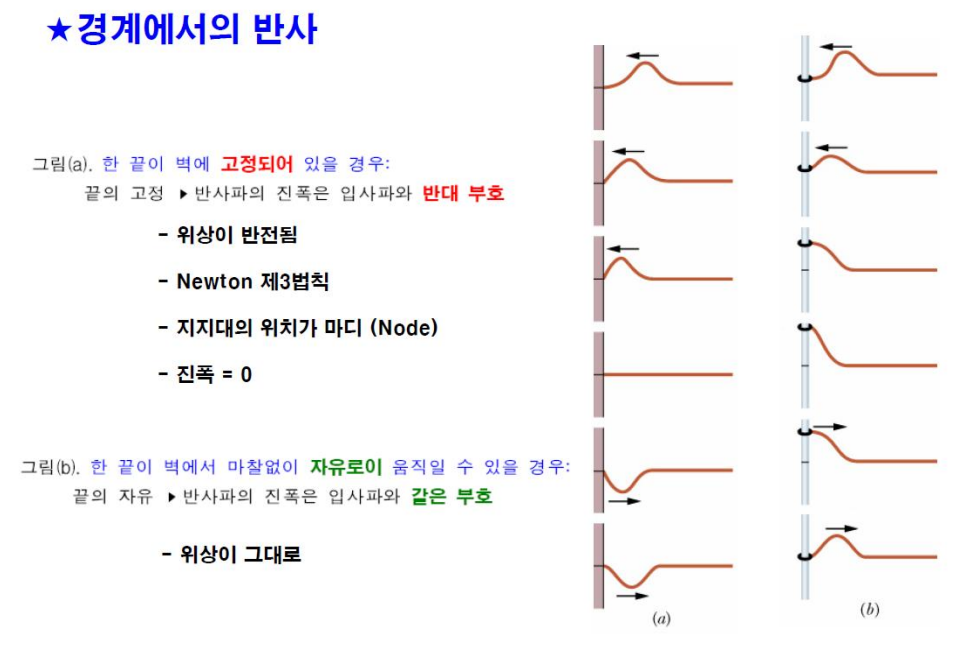
정상파, 정지파와 공명
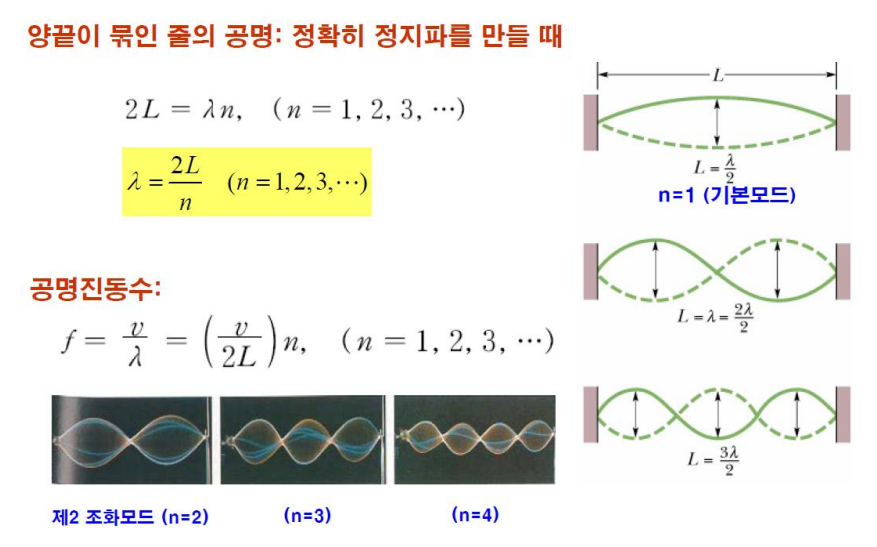
5. 음파
*음파 중 하나 시험문제 냄
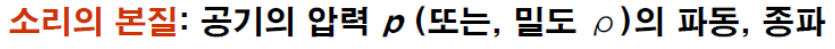
파면과 파선
1) 파면: 위상이 일정한 점들이 이루는 곡면
2) 파선: 파면에 대한 법선을 이은 곡선(에너지가 전달되는 궤적)
- 소리의 속력(음속)
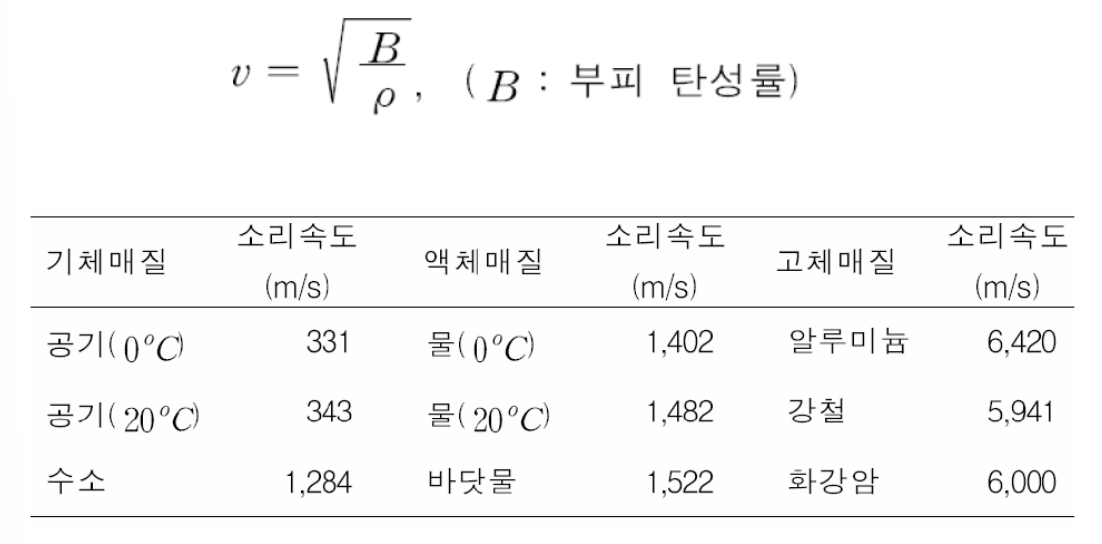
- 세기와 소리준위

- 음악적인 소리샘
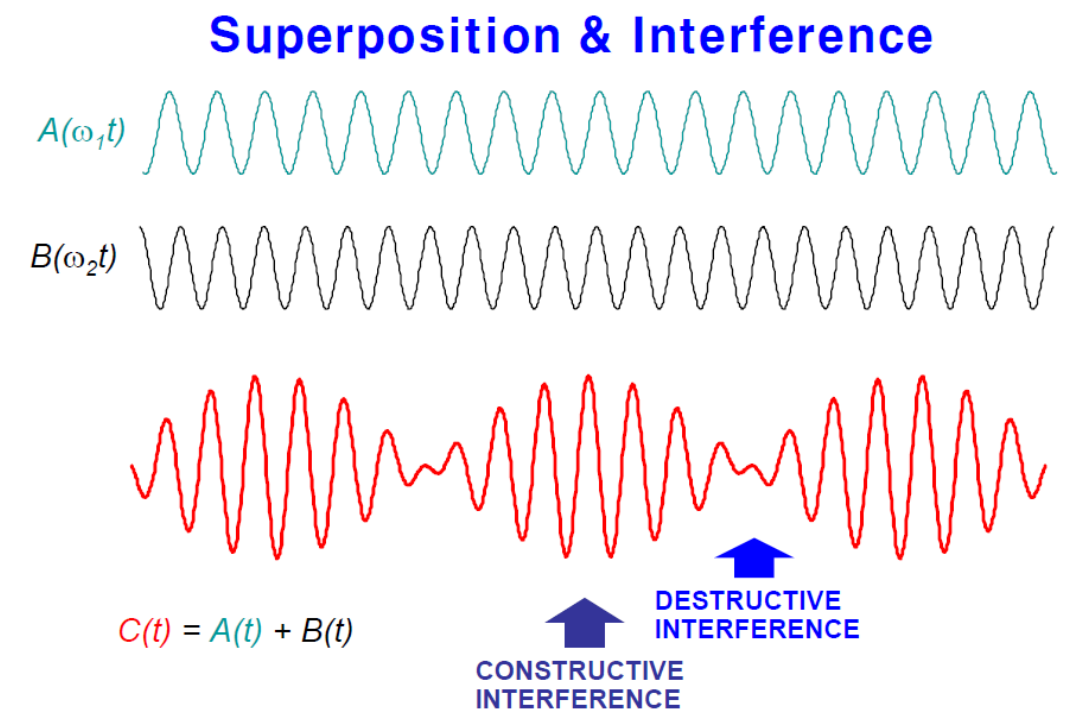
- 맥놀이(beats)

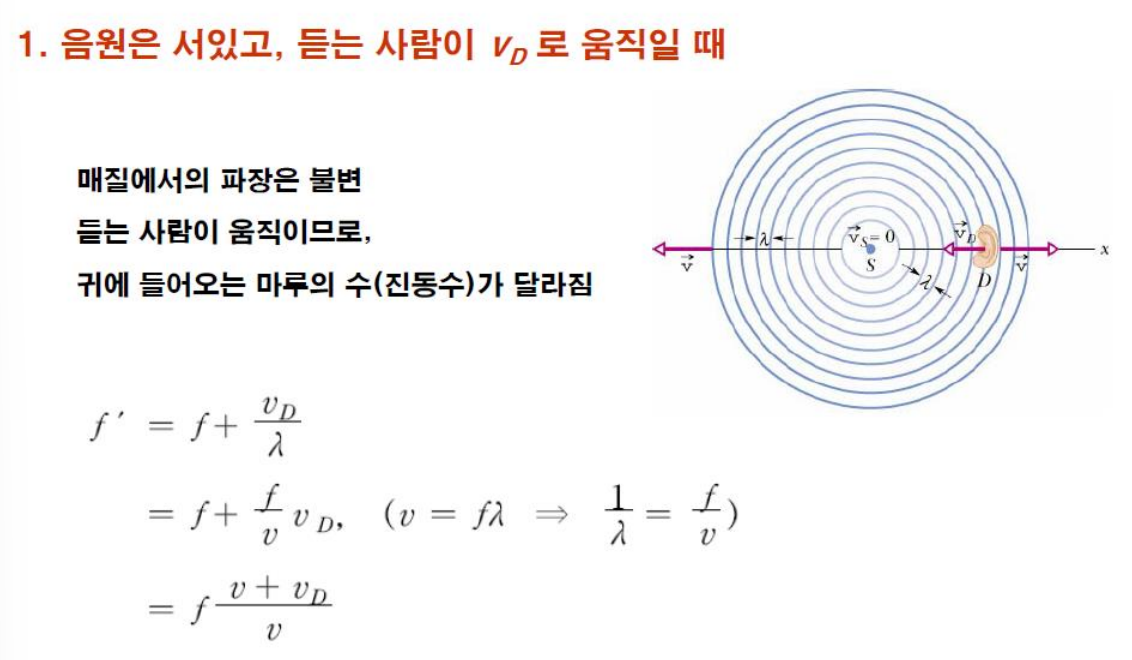
- 도플러 효과
* 시험에 나옴!!
* 시험에는 2개의 situation중 하나 낼 것임!
- 앰뷸런스가 서 있고 나는 움직인다. - 내가 움직이기 때문에 파면끼리의 간격이 일정
- 음원이 움직이므로 매질에서의 파장이 달라진다. 람다
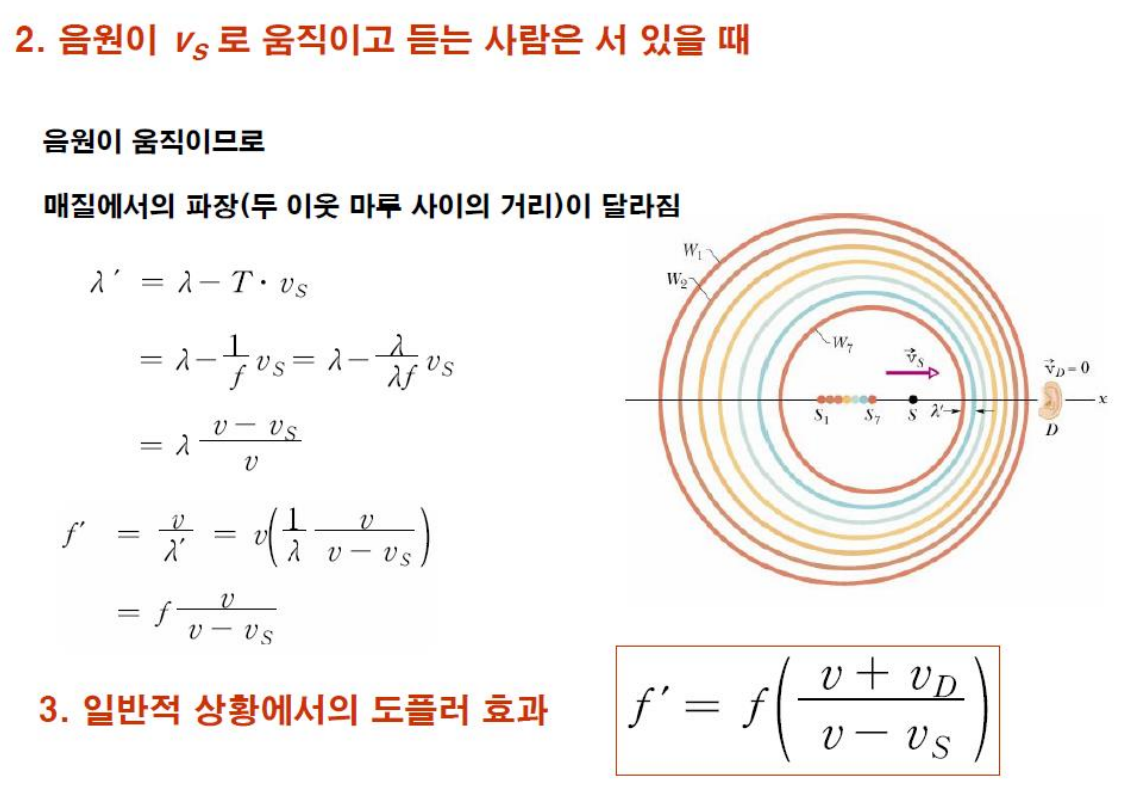
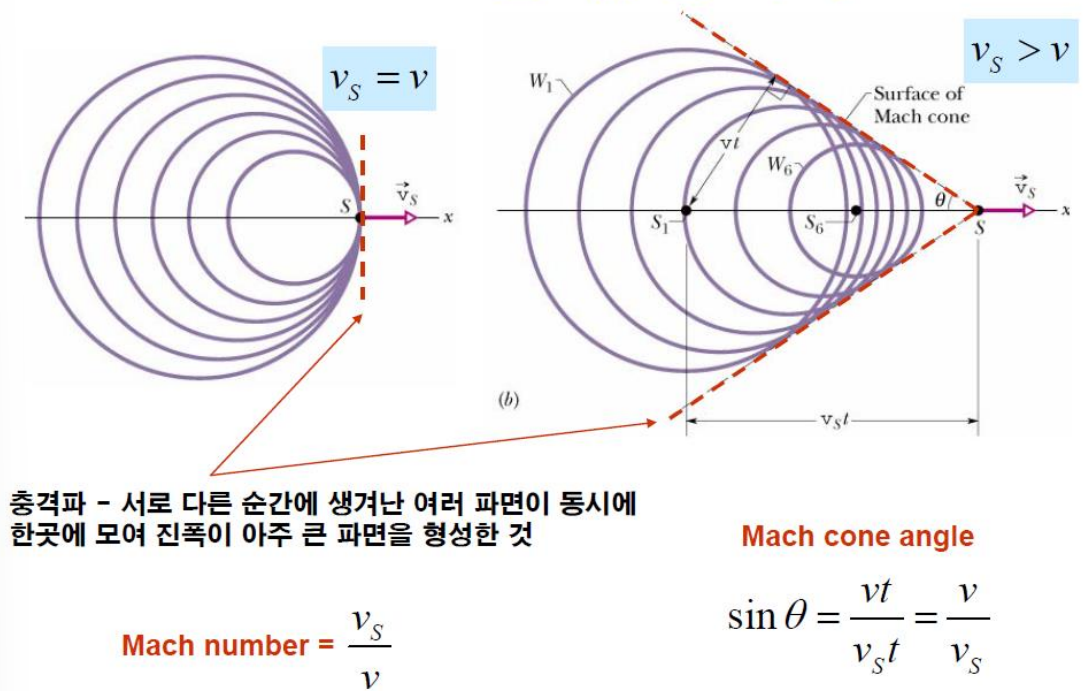
- 초음속, 충격파
6. 엔트로피
- 계(system)의 물리학
- 많은 입자가 만들어냄
- 입자가 많고 부피가 크고 열적 평형에 도달할 수 있는 계
- 1개의 입자, 질점에 대한 물리학과 질적으로 다른 내용
- 기체, 액체, 고체와 같이 물체의 상태에 관련한 여러 거시적인 정보(온도, 압력, 부피, 입자수, 화학포텐셜, 엔트로피......) 알아내기가 목표
- 많은 입자가 만들어냄
- 엔트로피
- 예시
- - 검은 콩 한 상자와 하얀 콩 한 상자를 섞어서 열어 보면 항상 검은 콩과 하얀 콩은 고르게 섞여 있는 것 으로 보인다. - 뜨거운 물과 차가운 물을 섞으면 항상 미지근 한 물이 된다. 뜨거운 물은 더 뜨겁게 차가운 물은 더 차 갑게 되는 경우는 볼 수 없다. - 영화에서 그릇이 깨졌다가 다시 합쳐지는 장면이 나온다면 우리는 영화를 거꾸로 돌리고 있음을 확신할 수 있다. - 쉬는 시간에 운동장에 뛰노는 초등학생들이 줄을 맞추어 움직이는 것은 절대로 있을 수 없다. - (시험에 나옴)주사위 100개를 동시에 던져서 모두 1이 나오는 경우는 거의 절대로 없다. 확률적으로 6의 100제곱분 의 1 ~ 10의 78제곱분의 1 !!!! (그러나, 살다보면 있을 수 있고 이런 경우를 기적이라고 한다.) 주사위 100개를 던지면 그 합이 거의 대부분 350 또는 351 또는 349가 나온다. - 포커에서 최고의 패는 로얄스트레이트플러쉬 (같은 무늬 10, J, Q. K, A)이고 확률적으로 약 65만분의 1 이다. 그냥 잡패들은 무늬가 같지도, 순서대로 나오지도, 짝을 짓지도 않은 그런 패들이다. 이런 잡패들은 가장 엔트로피가 높은 패들이다!!!!
- 예시
(1) 주사위 2개(시험에나옴)
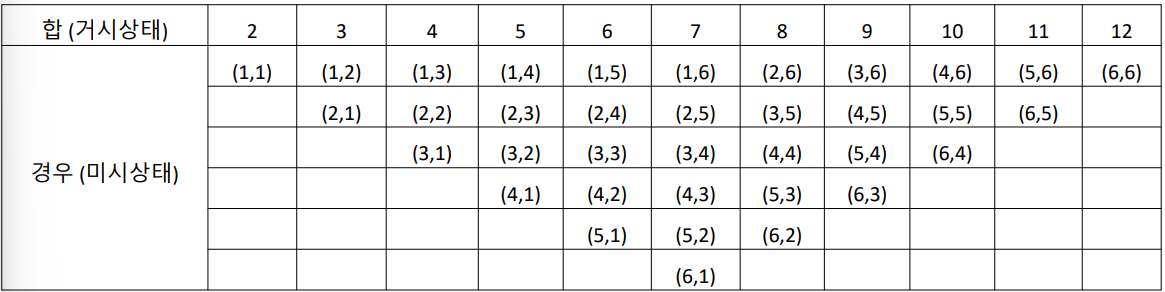
- 엔트로피가 크다 -> 거시상태에 대응하는 미시상태의 수가 많다.

(2) 열역학 함수
- U 내부에너지 (엔트로피를 고려한 열역학계의 에너지)
- H 엔탈피
- G Gibbs 자유에너지
- F Helmholtz 자유에너지
----> 모두 엔트로피를 고려하는 거시상태 함수
- 온도
- 열역학제0법칙: 온도가 존재한다.(열적 평형상태가 존재한다.)
- (중요) 열역학제1법칙: 에너지 보존의 법칙 (에너지는 새로 만들어지거나 없어지지 않는다. 형태가 변할 뿐이다.)
- (중요) 열역학제2법칙: 엔트로피 증가의 법칙 (비가역현상이 존재한다. 열손실 없이 모든 열을 일로 바꾸는 것은 불가능하다. 외부에서 일을 해주지 않으면 저온부에서 고온부로 열을 빼내는 것 은 불가능하다.....)
- 열역학제3법칙: 온도가 절대온도 0도로 가까이 가면 엔트로피는 0에 접근한다.
(1) 온도의 측정
- 열팽창 (수은온도계)
- 저항의 온도의존성 (실리콘온도계)
- 열기전력 (Thermoelectric Power: Thermopile)
(2) 온도에 따른 상전이
- 기체 (수증기) - 액체 (물) - 고체 (얼음)
- 상전이 온도는 물질에 특이하게 정해져 있음
- 구조상전이는 항상 잠열 (latent heat)을 동반한다. 이러한 구조상전이는 1차 상전이라고 한다. 연속적인 상전이는 잠열이 없고 2차 상전이라고 부른다.
(3) 온도-압력-부피의 관계
- PV = kT (보일-샤를의 법칙)
7. 열역학 법칙
- 열과 일: 열역학제1법칙(에너지의 보존)

- 이상기체의 비열
- 단원자 이상기체 : 실제로 존제하지 않지만 헬륨이 가장 가까움
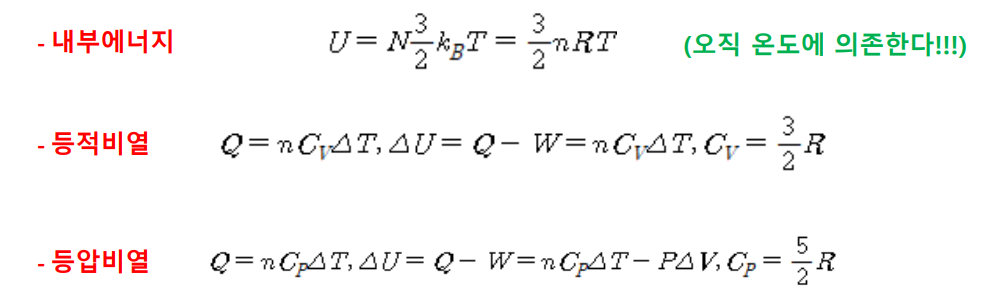

- 단열과정
- cf. 등온과정 (isothermal process) PV = nRT = constant
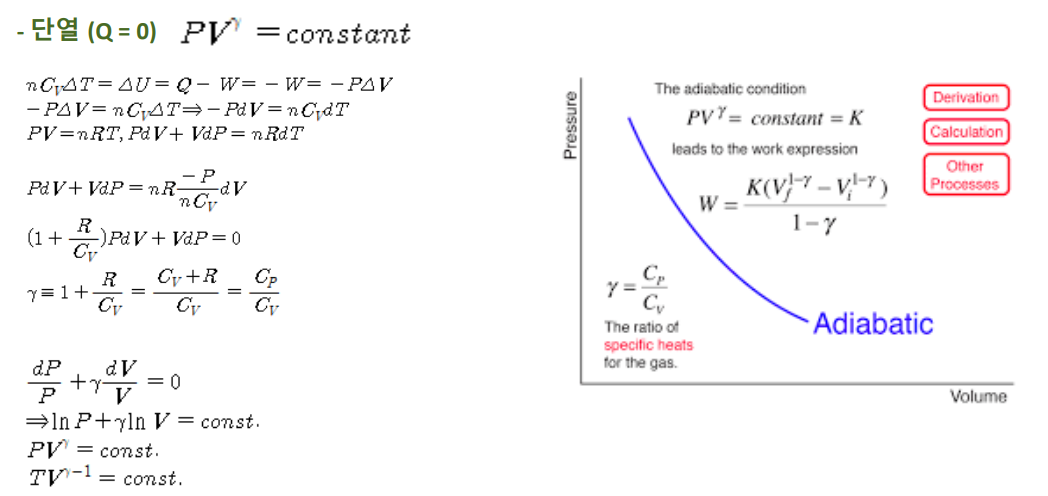
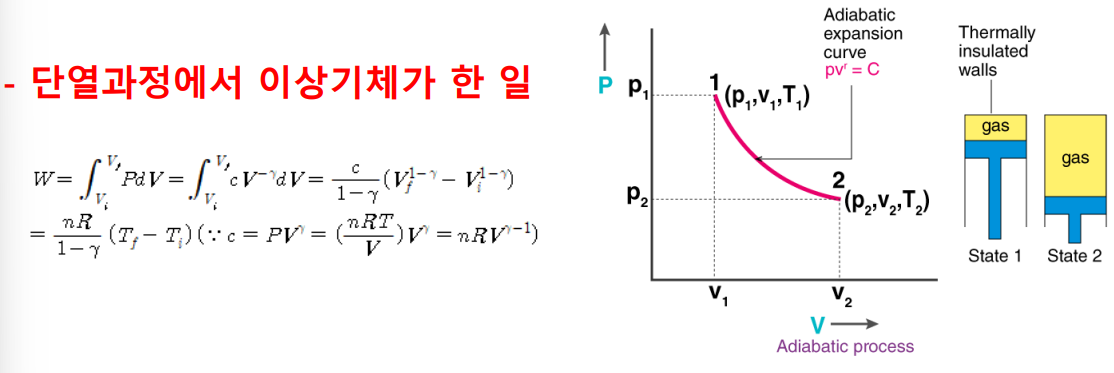
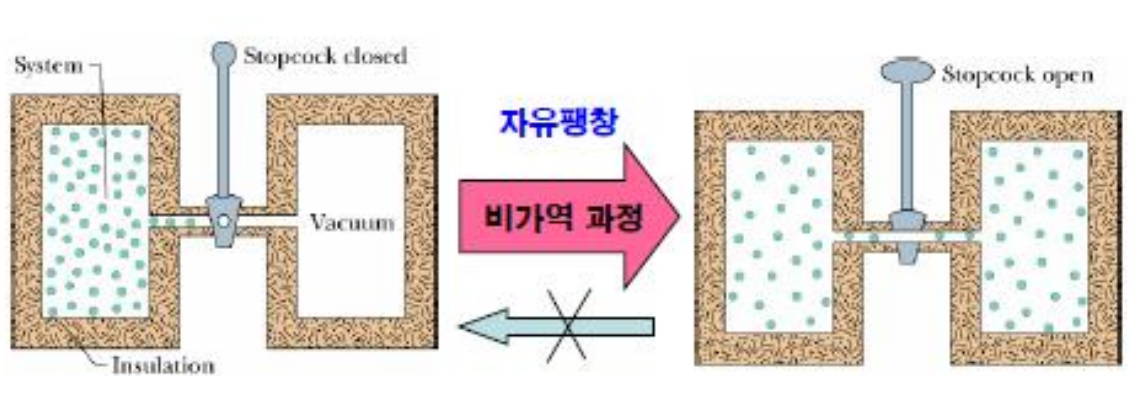
- 비가역과정 vs 가역과정
- 자유팽창 (free expansion)
- Joule-Thomson 팽창



- 열기관과 열효율
- 열기관 (heat engine) : 주위에서 열에너지를 받아 일을 되풀이하는 장치 (순환과정 cycling!)
- 열기관의 효율

- 냉각기의 효율

8. 이상기체
- 기체의 압력의 근원 = 기체분자의 열 운동
- 기체가 담긴 그릇의 벽면이 받는 압력은 열 운동하는 기체분자가 벽면과 부딪치면서 전달하는 운동량으로부터 생긴다.
- 하나의 기체분자 (i-번째)가 갖는 x-축 방향 운동량의 변화량
- Gases의 키네틱이론


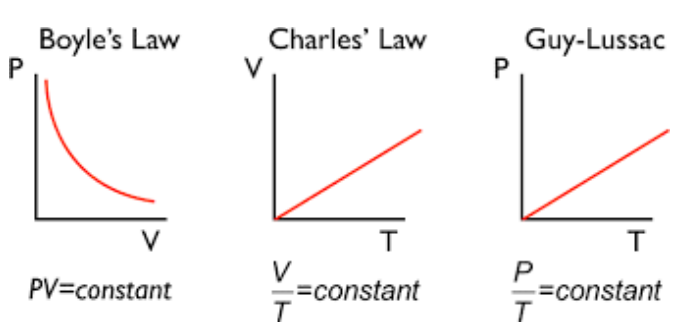
- 이상기체
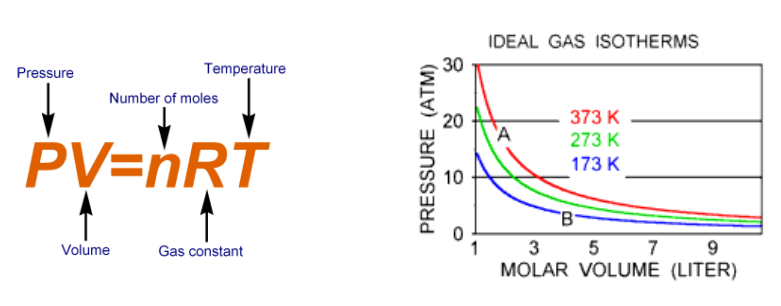
- 상태방정식 (Equation of State)
- PV = nRT (n 몰수, R 기체상수) = NkB T (N 입자수, kB 볼쯔만상수)
- 입자의 크기를 무시할 수 있다.
- 모든 충돌은 탄성충돌이다.
- 이상기체는 실제로는 존재하지 않는다.
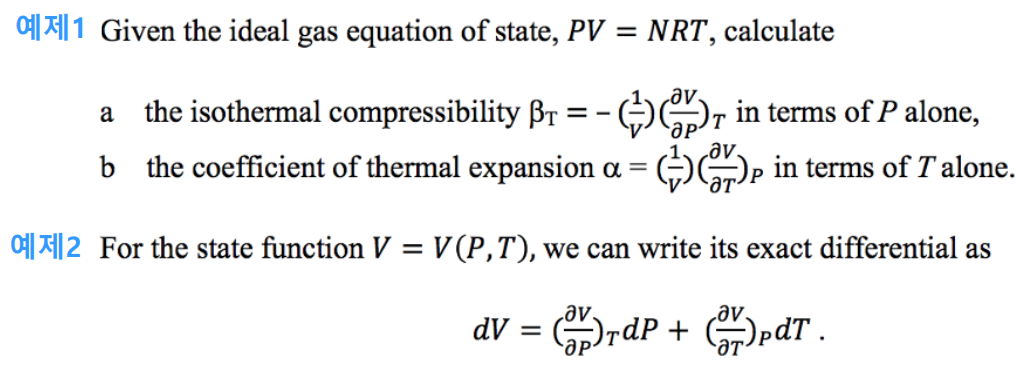
'EWHA > 24-2' 카테고리의 다른 글
| [일반물리학] PPT 개념정리 (2) | 2024.10.28 |
|---|---|
| [일반물리학] chap3. 벡터 (2) | 2024.10.03 |
| [일반물리학] chap2. 일차원에서의 운동 (1) | 2024.10.02 |